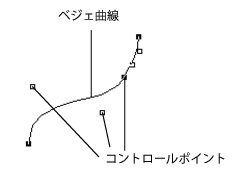
ベジェ曲線

JSLには、曲線や曲面とそれに対するメッシュを定義・描画するためのコマンドが用意されています。本書では、ベジェ曲線についての詳しい説明は省略します。

図13.19 ベジェ曲線 

1次元評価機能

1次元のベジェ曲線を定義するには、Map1関数を使います。

Map1( target, u1, u2, stride, order, matrix )

target引数には、制御点で何を表すかを定義します。target引数の値は、Table 13.6に示しています。Enableメッセージを送って、引数を有効にする必要があります。

2番目の2つの引数（u1とu2）には、曲線の範囲を指定します。strideは、記憶されている制御点の、各ブロックごとの数値の個数（つまり、ある制御点から、次の制御点までのオフセット）です。orderは、曲線の次数に1を足した値です。matrixには、制御点を指定します。

たとえば、Map1( MAP1_VERTEX_3, 0, 1, 3, 4, <4x3 matrix> )のように指定します。これは、2つの端点に対し、制御点を2つ設定してベジェ曲線を定義する典型的な方法です。

MapGrid1とEvalMesh1関数を使って、等間隔のメッシュを定義し、適用します。

MapGrid1( un, u1, u2 )

このコマンドは、u1からu2の範囲にわたってun分割されるメッシュをセットアップします。0から1までを範囲とすれば、コーディングが簡素化されます。

EvalMesh1( mode, i1, i2 )

このコマンドは、i1からi2まで実際にメッシュを生成します。modeには、POINTまたはLINEを指定できます。EvalMesh1関数は、固有のBegin節およびEnd節を作成します。

次のスクリプト例では、ベジェ曲線を描きます。乱数によって決められた制御点をもとに、滑らかな曲線が描かれます。最初と最後の点だけが曲線上にあります。NPOINTS=4を指定していますので、3次のベジェ曲線が描かれています。

boxwide = 500;

boxhigh = 400;

gridsize = 100; // 値を大きくすると、より見やすい間隔になる

/* 2以上8以下の値を指定してください。この範囲外の数値は、実装方法によっては正しく動作しないかもしれません。この値は、曲線の次数に1を足したものです。*/

NPOINTS = 4;

point = J( NPOINTS, 3, 0 );

// x、y、zの3次元配列を作成する

For( x = 1, x <= NPOINTS, x++,

	point[x, 1] = (x - 1) / (NPOINTS - 1) - .5;

// xの範囲は-.5～+.5

	point[x, 2] = Random Uniform() - .5; // yは同じ範囲の乱数

// 1つの平面上に曲線を描くので、zは常にゼロ

	point[x, 3] = 0;

);

spline = Scene Box( boxwide, boxhigh );

// xとyの範囲は-0.5～0.5なので、それよりわずかに大きくする

spline << Ortho( -.6, .6, -.6, .6, -2, 2 );

spline << Enable( MAP1_VERTEX_3 );

spline << MapGrid1( gridsize, 0, 1 );

spline << Color( .2, .2, 1 ); // 青色の曲線

spline << Map1( MAP1_VERTEX_3, 0, 1, 3, NPOINTS, point );

spline << Line Width( 2 ); // 細すぎない曲線にする

spline << EvalMesh1( LINE, 0, gridsize ); // LINEをPOINTに変更して試してください

spline << Color( .2, 1, .2 );

spline << Point Size( 4 ); // 大きい緑色の点

// 点を表示してラベルを付ける

For( i = 1, i <= NPOINTS, i++,

	spline << Begin( "POINTS" );

	spline << Vertex( point[i, 1], point[i, 2], point[i, 3] );

	spline << End;

	spline << Push Matrix;

	spline << Translate( point[i, 1], point[i, 2], point[i, 3] );

	spline << Text( center, bottom, .05, Char( i ) );

	spline << Pop Matrix;

);

New Window( "スプライン", spline );

https://www.tinaja.com/glib/bezconn.pdfでは、勾配と変化率が連結点で一致している、区分的な3次式を求める方法が説明されています。上記の例は区分的な曲線は1本だけで、複数の区分的な曲線を連結しているわけではありません。