LSVの計算

最小有意値（LSV）は、1次元の対比についてのみ計算されます。

単一の線形対比の検定

自由度が1つの検定Lb = 0を検討します。ここで、Lは、パラメータに対する制約を表す行ベクトルです。この仮説のt検定の検定統計量は次のとおりです。

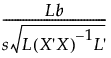
ここで、sは誤差の標準偏差（RMSE; Root Mean Square Error, 平均2乗誤差の平方根）です。この検定統計量の絶対値が、1 ‐ a/2におけるt分布の分位点t1‐α/2を超える場合、有意水準aにおいて仮説は棄却されます（このときの、t分布の自由度は誤差の自由度と同じです）。

最小有意値は、検定統計量がちょうどその棄却値になるときのLbの値で、次式によって求められます。

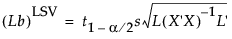
1個のパラメータに対する検定の場合

検定される対比が、1個のパラメータbiが0であることを帰無仮説とする場合には、そのLSVは次式のようになります。

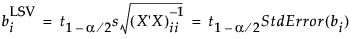
平均の差の検定

2群間の平均差に対する検定では、最小有意差（LSD; Least Significant Difference）という指標が使われることがあります。一元配置分散分析においては、LSDの計算式は、次のように簡単に求めることができます。

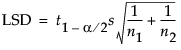
なお、JMPでは、名義尺度効果の各水準に対するパラメータは、その水準の平均から、全水準の平均を引いたものになっています。このコード化においては、LSVは、LSDを半分したものになっています。

メモ: 名義尺度の効果に対比を指定する場合、JMPで採用されている名義尺度のコード化に注意しながら対比を指定してください。JMPのコード化では、ある1水準に対するパラメータは、その水準の平均から、全水準の平均を引いた差になっています。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).