潜在成長曲線モデルの例
潜在成長曲線モデル(LGC model; latent growth curve model)は、経時的データに対して使われているモデルであり、時間の経過に伴う軌道をモデル化します。最もよく使われている潜在成長曲線モデルは、1次の潜在成長曲線です。1次の潜在成長曲線では、切片と傾きの潜在変数を指定して、母集団全体での切片と傾きの定数と、その集団での定数からの各個体のばらつきをモデル化します。潜在成長曲線モデルは、ランダム係数モデルに非常によく似ています。潜在成長曲線モデルでは、データの平均構造に制約を設けます。平均構造もモデル化することによって、母集団全体の傾向に関する仮説を検証できます。
この例では、4年におよぶ教育プログラムにおける生徒の成績をモデル化します。「1次式によってこの過程はよく表される」という仮説を検証してみましょう。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Academic Achievement.jmp」を開きます。
2. [分析]>[多変量]>[構造方程式モデル]を選択します。
3. 「複数選択 1年目」から「複数選択 4年目」まで選択し、[モデルの変数]をクリックします。
4. [OK]をクリックします。
「構造方程式モデル」レポートが開き、「モデルの指定」アウトラインが表示されます。
5. [モデルのショートカット]>[経時的データ分析]>[1次の潜在成長曲線]を選択します。
「モデルの指定」の図に、1次の潜在成長曲線モデルが表示されます。
6. パス図が表示されている画面右側にて、[リスト]タブをクリックします。
7. 「分散」リストの最初の4項目を選択し、[等号制約の設定]をクリックします。
これは、各変数の残差分散が等しくなるように制約を設けるもので、等分散性の仮定に似ています。構造方程式モデルでは、等号制約のない別のモデルもあてはめて、カイ2乗検定を使って比較することで、この仮定を検証することが可能です。
8. 「モデル名」の下のテキストボックスに、「誤差が等分散である1次の潜在成長曲線」と入力します。
9. [実行]をクリックします。
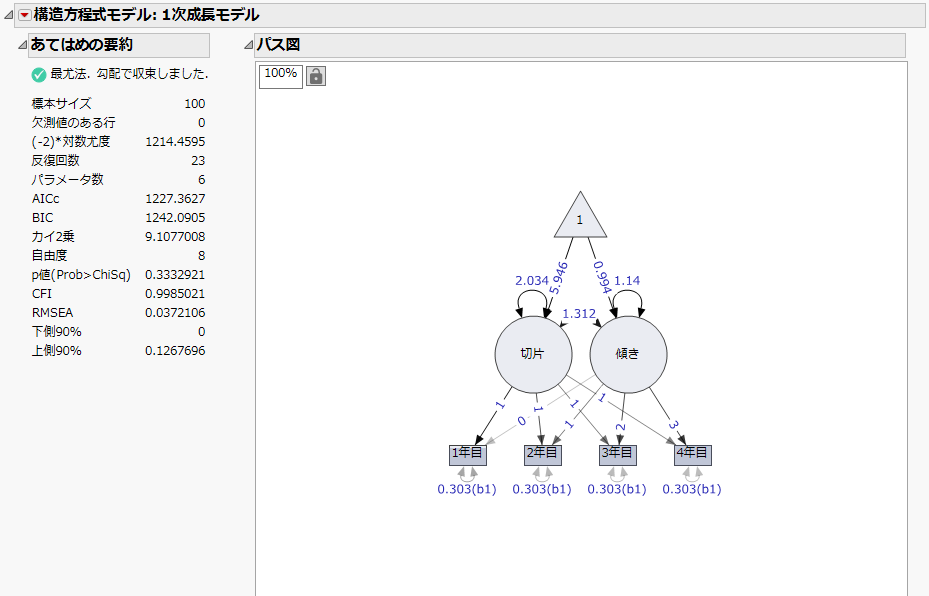
図8.11 1次の潜在成長曲線モデルの「あてはめの要約」と「パス図」
「あてはめの要約」によると、このモデルのカイ2乗は9.11、自由度は8です。p値は0.3333で、有意でないことに注目してください。これは、「観測された共分散行列に、このモデルは適合している」という帰無仮説を棄却する証拠はないということを示しています。したがって、「観測された共分散行列に、このモデルはあてはまっていないとは言えない」と結論できます。また、CFIは0.9より大きい値を、RMSEAは0.1より小さい値をとり、これらの適合度指標も非常にあてはまりが良いことを示しています。
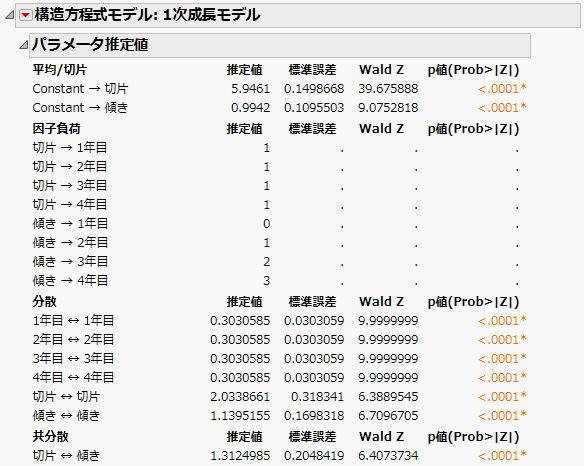
図8.12 1次の潜在成長曲線モデルの「パラメータ推定値」
切片の平均推定値は5.95です。これは、生徒全体における1年目の成績に対する予測値に該当します。つまり、「1年目の成績の生徒全体での平均は5.96である」ということができます。1年目の成績に対する傾きの負荷量は0になっています。よって、切片の推定値がそのまま1年目の成績の予測値となります。
傾きの平均推定値は0.99です。これは、生徒全体においては、成績スコアが毎年0.99ずつ伸びていることを示しています。切片および傾きの因子の分散推定値が有意であることは、平均や傾きには生徒ごとにばらつきがあることを示唆しています。つまり、調査開始時の成績や、成績の伸び率は、生徒ごとに異なります。何かしらの外生的な変数を切片や傾きの説明変数として取り入れることによって、個々の軌道の差をもたらしている要因を調べることができます。
なお、切片と傾きの共分散が正になっていることは、1年目に成績が良かった生徒は、毎年の伸び率も高いということを示しています。
潜在成長曲線モデルを使えば、時間の経過に伴う過程の変化について柔軟に調べることができます。「モデルのショートカット」メニューには、成長なしの軌道のほか、2次の軌道や、非線形の軌道([潜在基底成長曲線]オプション)もあり、これらの異なる軌道をあてはめて互いに比較し、最もあてはまりの良いモデルを判断することができます。