並び替え検定の例
この例では、乱数シミュレーションに基づいて、並び替え検定を行ってみましょう。3種類の鎮痛剤の効果に違いがあるかどうかに興味があります。標本サイズが非常に小さく、通常の分散分析では妥当な結果とならない恐れがあります。そこで、シミュレーションに基づく並び替え検定を行ってみましょう。
まず、痛みの程度の測定値を、3種類の薬に対してランダムにシャッフルする計算式を作成します。「鎮痛剤の効果がない」という帰無仮説のもとでは、観測された測定値に対して各処置が同様の確率で割り付けられると考えられます。測定値をランダムにシャッフルして得られるF値は、標本サイズが大きければ近似的にF分布に従います。ここでは、通常の分散分析のようにF分布からp値を計算するのではなく、乱数による並び替えによってp値を求めてみましょう。
シミュレーションの計算式の定義
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Analgesics.jmp」を開きます。
2. [列]>[列の新規作成]を選択します。
3. 「列名」に「痛みの程度(シャッフル)」と入力します。
4. 「列プロパティ」リストから[計算式]を選択します。
5. 関数のリストから[行]>[Col Stored Value]を選択します。
6. 「列」のリストから、[痛みの程度]をダブルクリックします。
7. エディタパネルの上部の記号リストから、挿入キー(^)をクリックします。
8. 関数のリストから、[乱数]>[Col Shuffle]を選択します。
図10.9 完成した式
この計算式は、「痛みの程度」列の値をランダムにシャッフルします。
9. 計算式エディタウィンドウで[OK]をクリックします。
10. 列情報ウィンドウで[OK]をクリックします。
並び替え検定の実行
1. [分析]>[二変量の関係]を選択します。
2. 「痛みの程度」を選択し、[Y, 目的変数]をクリックします。
3. 「薬」を選択し、[X, 説明変数]をクリックします。
4. [OK]をクリックします。
5. 赤い三角ボタンをクリックし、[平均/ANOVA]を選択します。
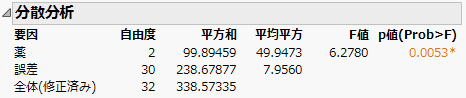
図10.10 「分散分析」レポート
ここで、F値が6.2780であることに注目してください。
6. 「分散分析」アウトラインの「F値」列を右クリックし、[シミュレーション]を選択します。
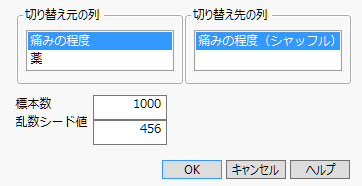
7. 「切り替え元の列」のリストから、「痛みの程度」をクリックします。
8. 「切り替え先の列」のリストから、「痛みの程度(シャッフル)」をクリックします。
9. 「標本数」に「1000」と入力します。
10. (オプション)「乱数シード値」に「456」と入力します。
こうすると、後述する結果と同じ結果が再現されます。
図10.11 設定後の「シミュレーション」ウィンドウ
11. [OK]をクリックします。
シミュレーションの結果を示すテーブルでは、「全体(修正済み)」と「誤差」は空白になっています。F値だけが、「薬」の列に出力されています。
12. このテーブルで、「一変量の分布」スクリプトを実行します。
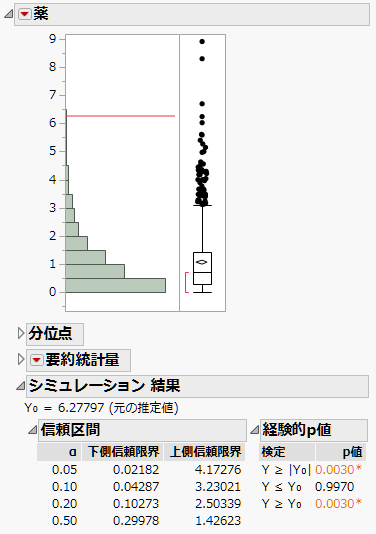
図10.12 シミュレーションによって得たF値の帰無分布
観測されたF値の6.2780は、ヒストグラムにおいて赤い線で表示されます。この値は、シミュレーションによって得たF値の帰無分布における上位0.5%点よりも大きくなっています。このことより、今回の実験結果は、「3種類の薬が痛みの程度に与える効果のいずれかは異なる」ことを示す強い証拠であると言えます。