2項分布に対するプロビットモデルの例

「非線形回帰」プラットフォームの数値微分を使用すると、2項分布に対するプロビットモデルの最尤法による推定値を得ることができます。この例で使用するデータテーブルは、製造過程で加熱時間とソーキング時間を変えながら、圧延に耐える状態に仕上がったインゴットの数を記録したものです。圧延に耐えるインゴットの平均数は、与えられた加熱時間とソーキング時間においてインゴットが良い状態に仕上がる確率に、検査された数を掛けたものです。

1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Ingots2.jmp」を開きます。

2. ［分析］>［発展的なモデル］>［非線形回帰］を選択します。

3. 「モデル変数(P)」を［X,予測式列］に指定します。

プロビットモデルをあてはめるために、サンプルデータの「モデル変数(P)」列には次の計算式が設定されています。

Normal Distribution(b0+b1*Heat+b2*Soak)

Normal Distribution関数の引数は、2変数の線形モデルになっています。

4. 「損失関数」を［損失］に指定します。

ニ項誤差を指定するために、「損失関数」列には次のような損失関数が含まれています。

-(適合数*Log(p)+(全体数-適合数)*Log(1-p))

5. ［数値微分のみ］チェックボックスをオンにします。

6. ［OK］をクリックします。

7. ［実行］をクリックします。

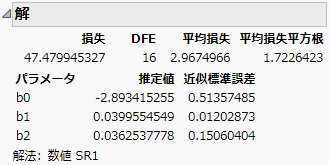
ここでは、数値微分を反復計算で使用しました（Figure 15.17）。

図15.17 「Ingots2」データの解 

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).