構造方程式モデルの例
この例では、ある企業の人事部が、職場の状況について評価するために、アンケート調査を行おうとしています。そのために、まずは「構造方程式モデル」プラットフォームを使って、確証的因子分析モデルを作成します。その確証的因子分析モデルを使って、200人の社員から得たアンケート調査への回答を分析します。このアンケート調査には、業務満足度のさまざまな側面に関する11個の質問が含まれています。確証的因子分析モデルによって、調査への回答を、リーダーシップの要素、役割の葛藤、全体的な業務満足度という3つの潜在変数に関連付けます。
1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Job Satisfaction.jmp」を開きます。
2. ［分析］>［多変量］>［構造方程式モデル］を選択します。
3. ［Support_L］から［Supervisor_S］までを選択し、［モデルの変数］をクリックします。
4. ［OK］をクリックします。
「構造方程式モデル」レポートが開き、「モデルの指定」アウトラインが表示されます。
潜在変数の作成
5. 「矢印の先」で、［Support_L］から［Interact_L］までを選択します。「矢印の先」リストの下のボックスに「Leadership」と入力し、
ボタンをクリックして潜在変数を追加します。
6. 「矢印の先」で、［Person_C］から［Inter_C］までを選択します。「矢印の先」リストの下のボックスに「Conflict」と入力し、 ボタンをクリックして潜在変数を追加します。
7. 「矢印の先」で、［General_S］から［Supervisor_S］までを選択します。「矢印の先」リストの下のボックスに「Satisfaction」と入力し、 ボタンをクリックして潜在変数を追加します。
共分散の追加とモデルのあてはめ
8. 「矢印の元」と「矢印の先」の両方で、［Leadership］・［Conflict］・［Satisfaction］を選択します。双方向の矢印ボタン 
をクリックします。
9. 「モデルの指定」レポートの左上にある「モデル名」のテキストボックスに、「3因子の確証的因子分析」と入力します。
10. ［実行］をクリックします。
11. （オプション）「構造方程式モデル: 3因子の確証的因子分析」の赤い三角ボタンをクリックし、［パス図の設定］>［レイアウト］>［上から下へ］を選択します。
12. （オプション）「パラメータ推定値」の横にあるグレーの開閉アイコンをクリックします。
「パラメータ推定値」レポートを閉じると、パス図の全体が見えるようになります。
13. パス図を右クリックして、［表示］>［推定値の表示］>［標準化］をクリックします。
モデルの標準化したパラメータ推定値がパス図に表示されます。
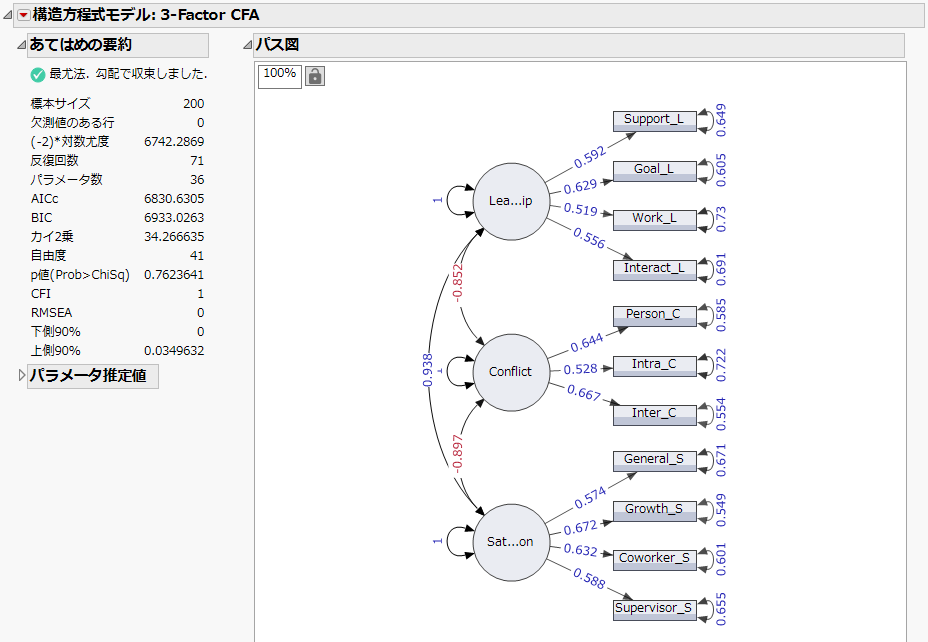
図8.2 「構造方程式モデル」レポート
「あてはめの要約」によると、このモデルのカイ2乗は34.27、自由度は41です。p値は0.7624と、有意ではないことに注目してください。これは、「観測された共分散行列に、このモデルは適合している」という帰無仮説を棄却する証拠はないということを示しています。したがって、「観測された共分散行列に、このモデルはあてはまっていないとは言えない」と結論できます。
カイ2乗値は標本サイズによって異なるので、よくあてはまっているモデルでも、有意になる場合があります。モデルの適合度を判断するその他の指標に、CFI（comparative fit index; 比較適合度指標）およびRMSEA（root mean square error of approximation; 近似の平均平方誤差平方根）があります。これらの指標は、0から1の間の値をとります。CFI>0.90およびRMSEA<0.10であることが、適合度の点では望ましいです（Browne and Cudeck 1993; Hu and Bentler 1999）。この例では、CFIは1であり、RMSEAは0です。よって、現在のモデルは得られたデータに良くあてはまっていると言えるでしょう。このアンケートが、「leadership」、「conflict」、「satisfaction」という潜在変数を測定するのに適切であると結論付けることができます。
14. 「構造方程式モデル: 3因子の確証的因子分析」の赤い三角ボタンをクリックし、［ヒートマップ］>［正規化した残差のヒートマップ］を選択します。
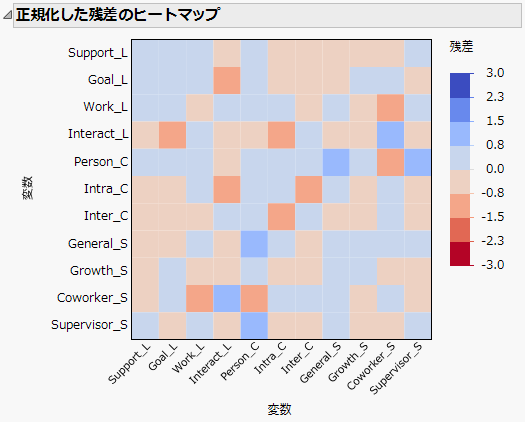
図8.3 正規化した残差のヒートマップ
「正規化した残差のヒートマップ」によると、正負の両方向において、2単位を超える正規化した残差はありません。これは、モデルがデータによくあてはまっていることをさらに裏付ける証拠となっています。正規化した残差によって、モデルのあてはまりの悪さをより細かく調べることができます。この例の正規化した残差からは、顕在変数間の共分散行列において局所的にあてはまりが悪くなっていることを示す証拠は見当たりません。