ラテン超方格計画の作成例

「Space Filling計画」プラットフォームを使って、4因子のラテン超方格計画を作成します。この結果を見ると、ラテン超方格法では、どの列（因子）にも各水準が1度ずつ割り当てられること、そして、どの列も水準の順序が異なることを確認できます。

1. ［実験計画(DOE)］>［特殊な目的］>［Space Filling計画］を選択します。

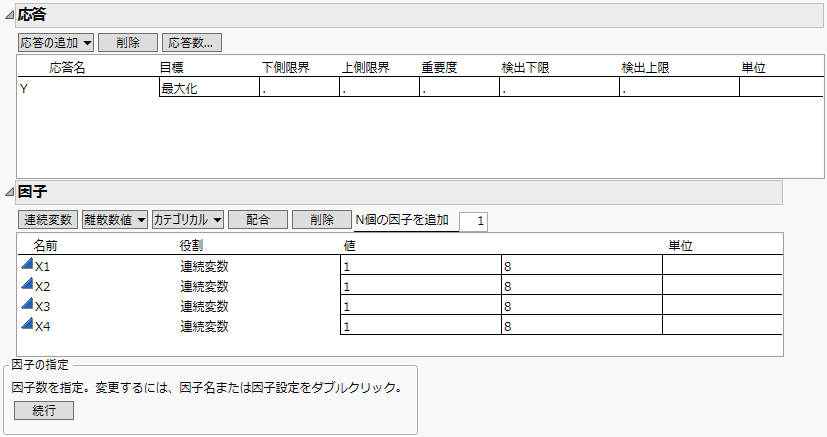
2. 連続尺度の因子を4つ追加し、値を1と8に変更します。

図22.8 因子が4つあるときの「Space Filling計画」ウィンドウ 

3. ［続行］をクリックします。

4. 「Space Filling計画手法」セクションで、「実験の回数:」に「8」と入力します。

5. ［ラテン超方格法］をクリックします。

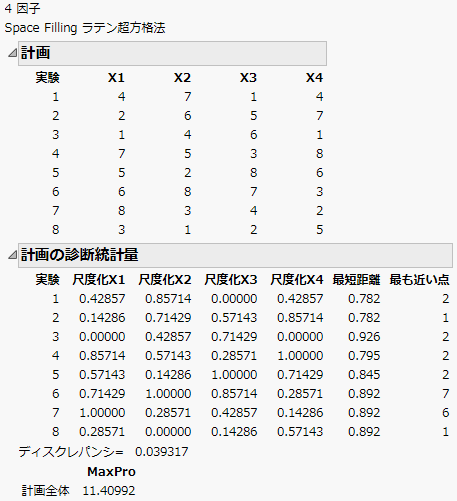
図22.9 ラテン超方格法による4因子8水準、実験数8の計画 

同じ因子数で比較したとき、ラテン超方格法では、2点間の最短距離が球の詰め込みの場合より短くなります。これは、ラテン超方格法には各因子の水準を均一に配置するという制約があるためです。球の詰め込みでは、何の制約もなく最短距離が最大化されます。