公開日: 09/19/2023
Space Filling計画
誤差によるばらつきが無視できるような場合には、Space Filling計画(空間充填計画)が役立ちます。Space Filling計画の種類としては、球の詰め込み、ラテン超方格法、一様、最小ポテンシャル、最大エントロピー、Gauss過程、高速柔軟充填があります。
コンピュータのシミュレーションモデルの感度を調べたい場合などがその一例です。また、機械論的モデルや決定論的モデルも、誤差によるばらつきがないので、Space Filling計画が役に立つでしょう。モデルに誤差によるばらつきがない場合、反復・ランダム化・ブロック化が不要になります。
「Space Filling計画」プラットフォームには、連続尺度の因子のみを含む計画が数種類用意されています。カテゴリカル因子・離散数値因子・配合因子を含む計画には、そのような因子に特化したSpace Filling計画も用意されています。連続変数だけを扱うSpace Filling計画の場合、主に、次の2つのアプローチがあります。
• 任意の2つの計画点の距離を最大化する。
• 点を一様な間隔で配置する。
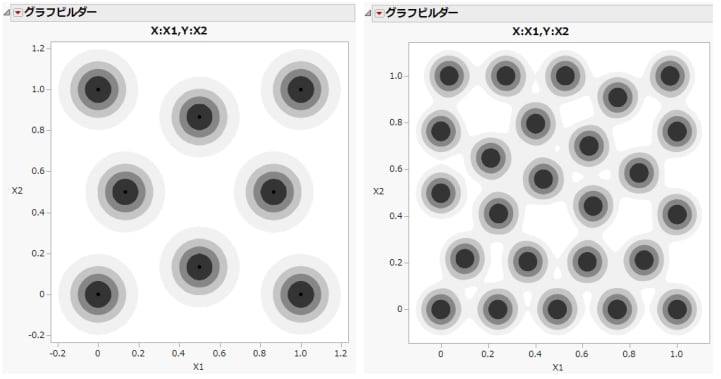
図22.1 Space Filling計画
目次
Space Filling計画の概要
Space Filling計画の例
Space Filling計画の作成
応答
因子
因子の制約を定義
Space Filling計画手法
計画
計画の診断統計量
計画のデータテーブル
Space Filling計画のオプション
Space Filling計画の別例
ラテン超方格計画の作成例
一様計画の作成例
球の詰め込み計画、ラテン超方格計画、一様計画の比較例
最小ポテンシャル計画の例
制約を指定した高速柔軟充填計画の例
地図上のSpace Filling計画の作成例
球の詰め込み計画の例
Space Filling計画の統計的詳細
最小ポテンシャル
最大エントロピー
Gauss過程 IMSE
高速柔軟充填計画の詳細
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).