Weibull損失関数をあてはめる例
この例では、「非線形回帰」プラットフォームによって、Weibull分布・対数正規分布・指数分布を生存時間データにあてはめる方法を紹介します。なお、この例では、2つの効果しか用いない単純なモデルをあてはめます。データには、名義変数「セル」などの効果もありますが、そのような名義変数を含むモデルを「非線形回帰」プラットフォームであてはめる場合には、ダミー変数も作成する必要があります。
最尤推定の最適化は、モデルパラメータの初期値によって大きく左右されることがあります。最尤推定の良い初期値として、最小2乗推定値を用いることが考えられます。以下では、まず、「非線形回帰」プラットフォームで最小2乗推定値を求めています。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「VA Lung Cancer.jmp」を開きます。
モデル式と、各確率分布に対する損失関数はすでにデータテーブルに計算式として作成されています。「モデル」列には次のような残差を表すモデル式が入っています。
Log(:生存日数)-(b0+b1*年齢+b2*月数)
2. [分析]>[発展的なモデル]>[非線形回帰]を選択します。
3. 「モデル」を[X, 予測式列]に指定します。
4. [OK]をクリックします。
5. [実行]をクリックします。
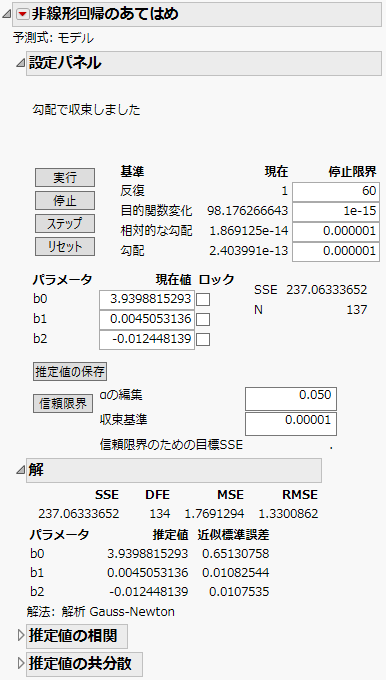
図15.24 「非線形回帰のあてはめ」設定パネルの初期パラメータ値
モデルパラメータの最小2乗推定値が計算されます。
6. [推定値の保存]をクリックします。
この操作により、最小2乗推定されたパラメータ推定値が、列の計算式に保存されます。
「Weibull損失関数」列には、Weibull分布の損失関数の計算式が指定されています。『信頼性/生存時間分析』のWeibull損失関数を参照してください。
最尤推定を行うには、次の手順に従います。
7. もう一度、[分析]>[発展的なモデル]>[非線形回帰]を選択します。
8. 「モデル」を[X, 予測式列]に指定します。
9. 「Weibull損失関数」を[損失]に指定します。
10. [OK]をクリックします。
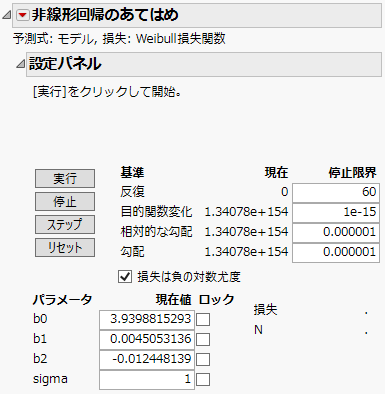
図15.25 最初の「非線形回帰のあてはめ」設定パネル
これを見ると、損失関数に「sigma」というパラメータが追加されているのがわかります。「sigma」は分数の分母に属するため、開始値を1とするのが適切です。デフォルト以外の損失関数を使っているときは、設定パネル上の[損失は負の対数尤度]チェックボックスはデフォルトでオンになります。
11. [実行]をクリックします。
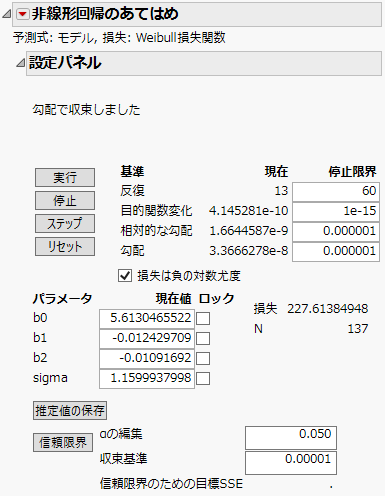
図15.26 非線形回帰のあてはめ
あてはめ処理では、Weibull分布の対数尤度の符号を逆にしたものを最大化するようなパラメータ推定値が計算されます。
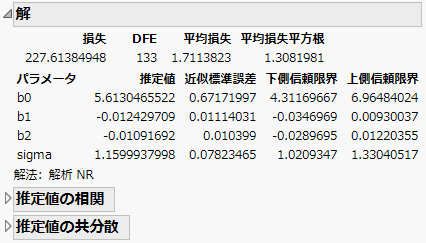
12. (オプション)[信頼限界]をクリックすると、パラメータの両側95%信頼区間の下限と上限が「解」表に表示されます。
図15.27 「解」レポート
メモ: この信頼区間は、普通の信頼区間(Wald法による信頼区間)ではなく、プロファイル尤度法によって計算されています。そのため、計算に時間がかかることがあります。
サンプルデータには、指数分布や対数正規分布の損失関数も保存されています。それらの分布をあてはめることもできます。新しい分布をあてはめる前に、最小2乗推定値を初期値に設定しておかないと、反復計算が収束しないことがありますので注意してください。パラメータ推定値をリセットするには、次の手順に従います。
13. (オプション)「非線形回帰のあてはめ」の赤い三角ボタンをクリックし、[元のパラメータに戻す]を選択します。