「生存時間(パラメトリック)のあてはめ」プラットフォームの統計的詳細
ここでは、「生存時間(パラメトリック)のあてはめ」プラットフォームで使用されている損失関数の統計的詳細について説明します。以下に挙げる損失関数は、よく使われる生存時間分布の「負の対数尤度」(対数尤度の符号を逆にしたもの)です。どの式も、計算式エディタのIf関数を使って表しています。If関数の初めの節で、打ち切られていないデータに対する損失関数が定義されています。続いて、右側打ち切りデータに対する損失関数がElse節で定義されています。これらの計算式は、サンプルデータフォルダの「Loss Function Templates」フォルダ内にあるデータテーブルからコピーして、分析対象とするデータテーブルに貼り付けることができます。
指数損失関数
ここに示す指数損失関数では、「sigma」は指数分布の平均、「時間」は故障時間です。
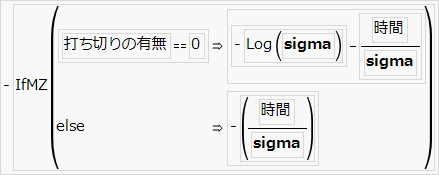
指数分布の特徴は、ハザード(瞬間故障率)が時間の経過に対して一定であることです。つまり、特定の期間にユニットが故障する確率は、ユニットがそれまでに経験した試験期間の長さに関係なく、常に一定です。
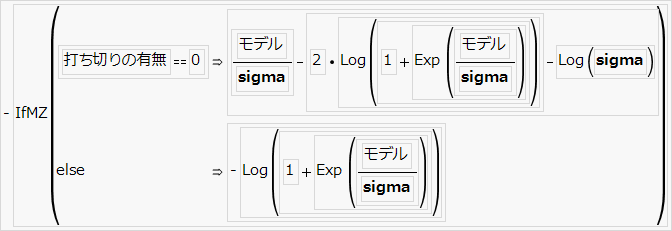
Weibull損失関数
Weibull分布は、寿命データを分析するのに多くの場面で適した分布です。Weibull損失関数がデータにとって適切かどうかを判断するには、[分析]メニューの[信頼性/生存時間分析]サブメニューの[生存時間分析]を用いることができます。
「Loss Function Templates」フォルダに、「モデル」列を使って定義する例(Weibull, 1 Parm.jmp)、2パラメータで定義する例(Weibull, 2 Parm.jmp)、極値分布(Extreme Value.jmp)の例が含まれています。
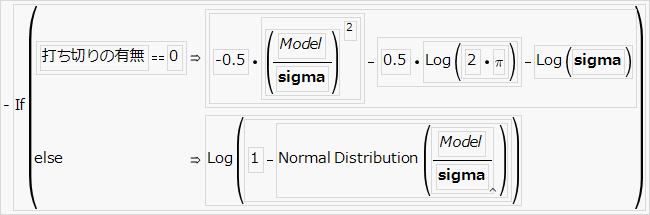
対数正規損失関数
下に示している対数正規損失関数の式において、Normal Distribution (モデル/sigma)は標準正規分布の累積分布関数です。対数正規分布のハザード関数はt = 0のときに0です。そして、tが大きくなるにつれて増加していき、最大値となるまで単調に増加します。、最大値に達した後は、tが大きくなるにつれて単調に減少し、0に近づきます。
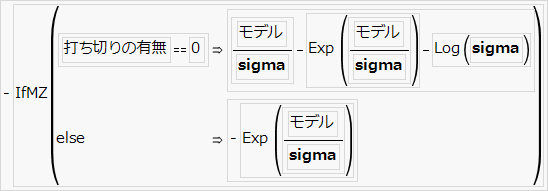
対数ロジスティック損失関数
Yがロジスティック分布に従う場合、exp(Y)は対数ロジスティック分布に従います。