偏相関係数行列の例
「多変量の相関」プラットフォームを使って、金属棒のコーティングの厚さを一定間隔ごとに調べます。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Quality Control」フォルダにある「Thickness.jmp」を開きます。
2. [分析]>[多変量]>[多変量の相関]を選択します。
3. 「厚さ」のすべての列を選択し、[Y, 列]をクリックします。
4. [OK]をクリックします。
5. (オプション)「多変量」の赤い三角ボタンをクリックして、[散布図行列]を選択し、散布図行列を非表示にします。
この例では散布図を使用しないので、非表示にして見やすくします。
6. 「多変量」の赤い三角ボタンをクリックし、[偏相関係数行列]を選択します。
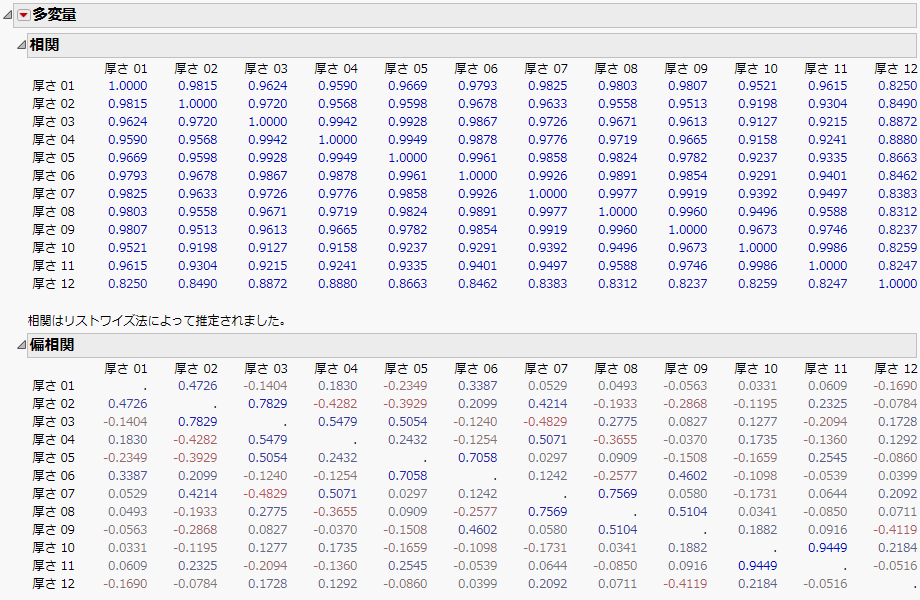
図3.8 厚さの相関係数と偏相関係数
偏相関係数行列を見ると、偏相関係数には正と負のものがあります。一方、相関係数行列を見ると、相関係数は正のもののみです。偏相関係数は、2変数間の関係において、他のすべての変数の効果を取り除いた後の相関係数です。そのため、相関係数と偏相関係数はこのような違いが生じます。相関係数だけでなく偏相関係数も見ることで、2変数間の関係をより詳しく把握できます。
7. 「多変量」の赤い三角ボタンをクリックし、[偏相関図]を選択します。
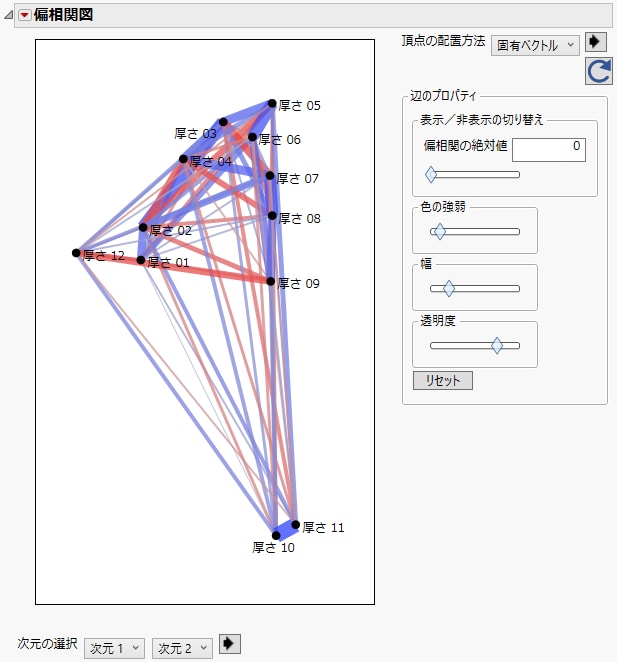
図3.9 偏相関図
偏相関図には、偏相関の様子が視覚的に表示されます。Figure 3.9の図には、厚さの各変数の頂点が表示されています。これらの座標は、次元1と次元2のスケールが調整された固有ベクトルに対応しています。厚さ10と厚さ11は、最初の2次元で近くに位置しており、他の厚さの変数とは離れています。また、厚さ10と厚さ11の頂点を結ぶ青い太線は、これらの変数間に正の強い偏相関があることを示しています。
その他の頂点はまとまって表示されており、解釈しづらいので、「偏相関の絶対値」に値を指定して、その値よりも偏相関が大きい線だけを表示することができます。
8. 「偏相関の絶対値」のボックスに「1」と入力します。
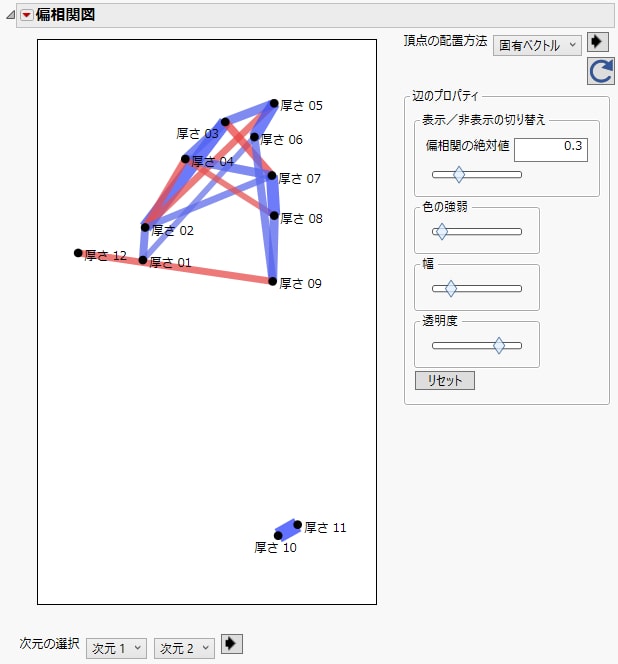
こうすると、図の線がすべて消えます。「偏相関の絶対値」の下にあるひし形をゆっくりと左にドラッグすると、偏相関が強い変数を見極められます。Figure 3.10の図には、偏相関が0.3よりも大きい2変数をつなぐ線が表示されています。
図3.10 0.3よりも大きい偏相関