非正規データのPpkに対する信頼限界のシミュレーションの例
この例では、まず非正規分布に従う3つの変数に対し、工程能力分析を行います。その後、シミュレーション機能を使用して、特定の変数の不適合率に対する信頼限界を求めます。
非正規分布の工程能力分析
以下の手順を自分で実行しなくても、「Tablet Measurements.jmp」に保存されている「工程能力」テーブルスクリプトを実行すれば、同じ結果が得られます。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Tablet Measurements.jmp」を開きます。
2. [分析]>[品質と工程]>[工程能力]を選択します。
3. 「重さ」・「厚さ」・「純度」を選択し、[Y, 工程変数]をクリックします。
4. 右側の「Y, 工程変数」リストで[重さ]、[太さ]、および[純度]を選択します。
5. 「分布オプション」アウトラインを開きます。
6. 「分布」リストから[最良]を選択します。
7. [工程分布の設定]をクリックします。
右側のリストにある列名に、「&分布(最良)」という接尾辞が追加されます。
8. [OK]をクリックします。
「工程能力指数プロット」が作成され、Ppkの値が表示されます。「厚さ」の変数だけが、Ppk = 1の線より上に位置しています。「純度」はほぼ線上にあります。測定値の個数は250で少なくないように思うかもしれませんが、Ppkの推定値はばらつきが大きくなっています。「純度」Ppk値に対する信頼区間を計算して、そのことを確認してみましょう。
メモ: なお、どの変数にとっても正規分布が最良の分布ではなかったので、ゴールプロットは表示されていません。
9. 「工程能力分析」の赤い三角ボタンをクリックし、[各列に対する詳細レポート]を選択します。
最良の分布は、工程変数ごとに異なります。
– 「重さ」: 対数正規
– 「厚さ」: SHASH
– 「純度」: Weibull
シミュレーション列の作成
シミュレーション機能を使ってPpkの信頼限界を推定するには、あてはめたWeibull分布を反映したシミュレーション計算式を作成する必要があります。以下の手順を自分で実行しなくても、「シミュレーション列の追加」テーブルスクリプトを実行すれば、同じ結果が得られます。
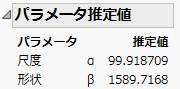
1. 下にスクロールして「工程能力 純度(Weibull)」レポートの「パラメータ推定値」レポートを見つけます。
図9.27 「純度」のWeibullパラメータ推定値
これは、最良の分布であるWeibull分布のパラメータ推定値です。
2. 「Tablet Measurements.jmp」サンプルデータテーブルで、[列]>[列の新規作成]を選択します。
3. 「列名」として「純度 乱数」とキーボードで入力します。
4. 「列プロパティ」リストから[計算式]を選択します。
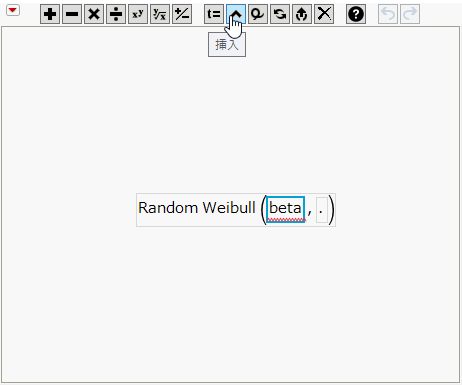
5. 計算式エディタで、[乱数]>[Random Weibull]を選択します。
6. 「beta」のプレースホルダーが選択されています。画面上部のアイコン一覧より、挿入アイコン(^)をクリックします。
図9.28 「純度 乱数」列の計算式エディタ
これで、alphaパラメータのプレースホルダーが追加されます。
7. 「工程能力」レポートの「工程能力 純度(Weibull)」で、「パラメータ推定値」レポートテーブルを右クリックし、[データテーブルに出力]を選択します。
8. 作成されたデータテーブルの2行目の「推定値」列の値をコピーします(1589.7167836)。
9. 計算式エディタウィンドウで、Random Weibull計算式の「beta」のプレースホルダーを選択し、
「1589.7167836」の値を貼り付けます。
10. 「パラメータ推定値」レポートから作成したデータテーブルで、1行目の「推定値」列の値をコピーします(99.918708989)。
11. 計算式エディタウィンドウで、Random Weibull計算式の「alpha」のプレースホルダーを選択し、
「99.918708989」の値を貼り付けます。
図9.29 入力後の計算式ウィンドウ
12. 計算式エディタウィンドウで[OK]をクリックします。
13. 「Tablet Measurements.jmp」データテーブルで、「純度 乱数」列を右クリックして、「列プロパティ」>「仕様限界」を選択します。
14. 「下側仕様限界」のボックスに「99.5」と入力します。
15. 「列の新規作成」ウィンドウで[OK]をクリックします。
「純度 乱数」列に、最良の分布から値をシミュレーションする計算式が設定されました。
「純度」のPpkの信頼区間と不適合率の期待値をシミュレートする
シミュレーション機能を使うと、分析全体が指定の回数だけ実行されます。必要な分析だけを実行し、計算の負担を減らせば、計算時間が短くなります。この例では、Weibull分布があてはめられた「純度」だけに興味があるので、シミュレート機能を実行する前に、「純度」の分析だけを行います。
メモ: 計算時間を気にしなければ、以前のセクションで作成した同じレポートを使用して、step 7を開始します。
1. 「工程能力分析」レポートで、「工程能力分析」の赤い三角ボタンをクリックし、[ダイアログの再起動]を選択します。
2. (オプション)「工程能力分析」レポートを閉じます。
3. 起動ウィンドウの「選択した列に役割を割り当てる」リストで、「重さ&分布(対数正規)」と「厚さ&分布(SHASH)」を選択します。
4. [削除]をクリックします。
5. [OK]をクリックします。
6. 「工程能力分析」の赤い三角ボタンをクリックし、[各列に対する詳細レポート]を選択します。
PpkとPplの両方の値が計算されていますが、値は同じです。なぜなら、「純度」には下側仕様限界しかないためです。
7. 「全体シグマ 工程能力」レポートで、「推定値」列を右クリックし、[シミュレーション]を選択します。
「切り替え元の列」リストで「純度」が選択されていることを確認します。「切り替え先の列」リストで「純度 乱数」が選択されていることを確認します。
8. 「標本数」に「500」と入力します。
メモ: 次のステップは、必須ではありません。ただし実行すると、この例で紹介しているのとまったく同じシミュレーション値を得ることができます。
9. (オプション)「乱数シード値」のボックスに、「12345」と入力します。
10. [OK]をクリックします。
計算には、多少時間がかかります。「工程能力 シミュレーション結果(推定値)」というデータテーブルが開きます。このデータテーブルにある「Ppk」と「Ppl」の各列には、「純度 乱数」の計算式に基づいて計算した500の値が含まれます。最初の行は、「純度」のデータに対して得られた元の値を含んでいます。この行の属性には除外が与えられています。「純度」は下側仕様限界しか持たないので、「Ppk」と「Ppl」の値は同じになります。
11. 「工程能力 シミュレーション結果(推定値)」データテーブルで、「一変量の分布」スクリプトの緑色の三角ボタンをクリックします。
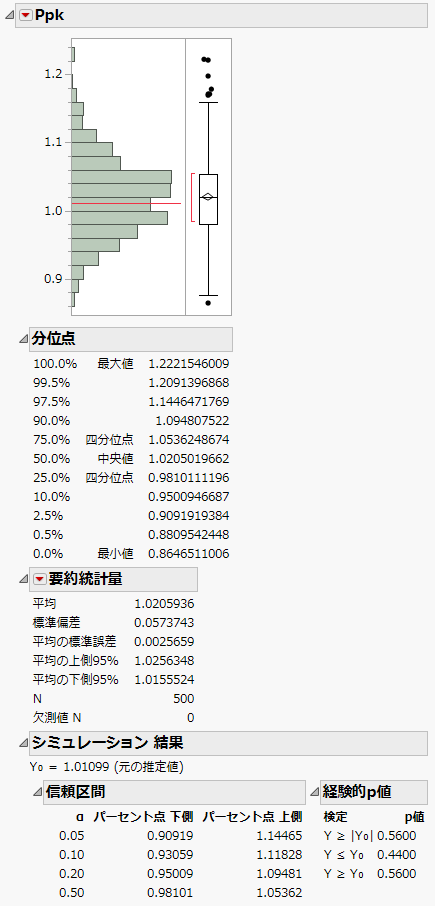
図9.30 シミュレーションで求めた「純度」のPpk値の分布
メモ: 「純度 乱数」列の計算式のパラメータの小数桁数精度により、値は表示とは若干異なることがあります。
PpkとPplの2つの「一変量の分布」レポートが表示されます。ただし、「純度」は下側仕様限界しか持たないため、PpkとPplの値は同じです。そのため、「一変量の分布」レポートも内容は同じです。
「シミュレーション 結果」レポートを見ると、Ppkの95%信頼区間は0.909~1.145です。これは次のことを示しています。真のPpkの値は、1.0より大きい可能性は否定できません。つまり、「純度」に対する結果は、非正規分布の工程能力分析で作成した「工程能力指数プロット」のPpk = 1の線より上に位置していることが考えられます。
12. 「工程能力分析」レポートの「不適合率」レポートで、「全体σ %」列を右クリックし、[シミュレーション]を選択します。
「切り替え元の列」リストで「純度」が選択されていることを確認します。「切り替え先の列」リストで「純度 乱数」が選択されていることを確認します。
13. 「標本数」のボックスに「500」と入力します。
14. (オプション)「乱数シード値」のボックスに「12345」を入力します。
15. [OK]をクリックします。
計算には、多少時間がかかります。「工程能力 シミュレーション結果(全体σ %)」というデータテーブルが開きます。「純度」には下側仕様限界しかないため、「LSL未満」の値は「限界外 合計」と一致します。
16. 「工程能力 シミュレーション結果(全体σ %)」データテーブルで、「一変量の分布」スクリプトの緑色の三角ボタンをクリックします。
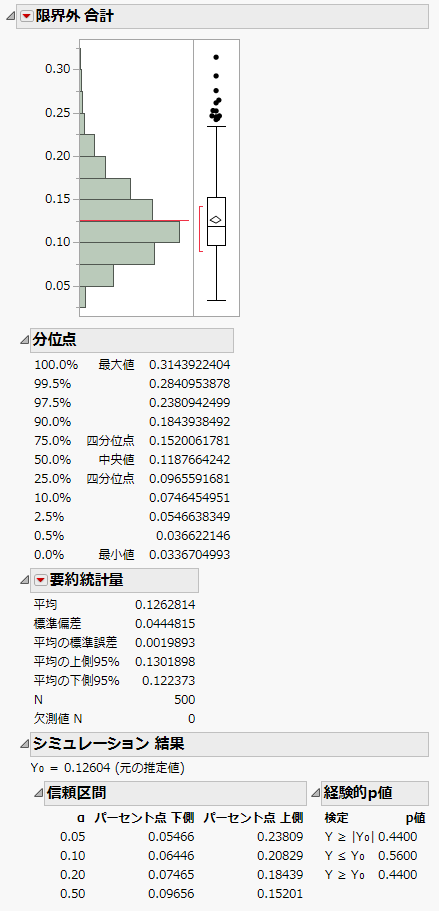
図9.31 「純度」の「限界外 合計」をシミュレーションした値の分布
メモ: 「純度 乱数」列の計算式のパラメータの小数桁数精度により、値は表示とは若干異なることがあります。
ここでも、同一の「一変量の分布」レポートが2つ作成されます。「シミュレーションの結果」レポートを見ると、不適合の「全体σ %」の95%信頼区間は0.055~0.238です。