ゼロ強調Poisson回帰の例
この例では、「モデルのあてはめ」プラットフォームで[一般化回帰]手法を使って、ゼロ強調Poisson回帰モデルをあてはめます。ゼロ強調Poisson分布は、度数データにおいて、度数がゼロとなる確率が通常のPoisson分布よりも多くなっている場合に適しています。
この例では、公園を訪れたグループが釣った魚の数に関するデータを分析します。サンプルデータには、公園を訪れた250グループについて、釣った魚の数に影響する可能性のある5つの因子が含まれています。
ただし、データの収集時には、グループ内の誰が実際に釣りをしたかどうかは特定されておらず、この列の情報は観測されていません。データの魚がゼロ匹である場合は、グループの誰も釣りをしなかったケースと、釣りをした人がいるが1匹も釣れなかったケースの2通りが考えられます。非表示の「釣りをした?」列には、どちらのケースに該当するかが含まれています。応答の度数が0であるのには、前述した2つの原因が考えられます。このような場合には、ゼロ強調分布が適しています。釣りをしたグループでの釣った魚の数にはPoisson分布が適しているため、ゼロ強調Poisson分布をあてはめます。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Fishing.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「列の選択」リストで「釣った魚」を選択し、[Y]をクリックします。
4. 「生き餌」から「子供」までを選択し、[マクロ]>[設定された次数まで]をクリックします。
2次までの項(「次数」ボックスでのデフォルト)がモデルに追加されます。
5. 「列の選択」リストで「検証」を選択し、[検証]をクリックします。
6. 「手法」のリストから[一般化回帰]を選択します。
7. 「分布」リストから[ゼロ強調 Poisson]を選択します。
8. [実行]をクリックします。
「一般化回帰」レポートが開き、「モデルの比較」レポート、「モデルの設定」パネル、「最尤法 (検証法: 検証列, 分布: ゼロ強調 Poisson)」レポートが表示されます。デフォルトの「推定法」はLassoになっています。
9. 「推定法」リストから[弾性ネット]を選択します。
10. [実行]をクリックします。
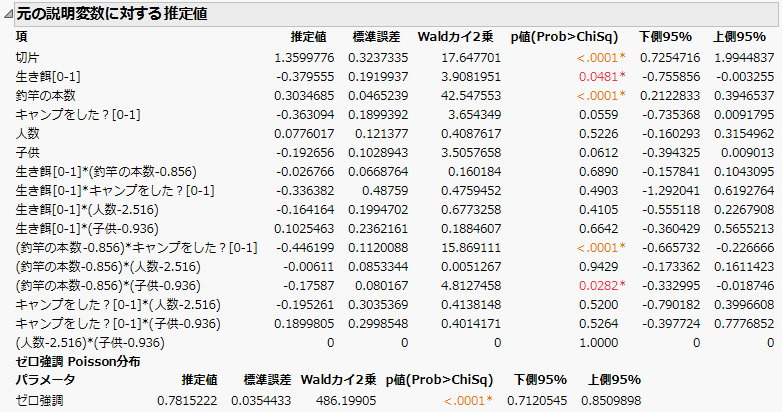
「弾性ネット (検証法: 検証列, 分布: ゼロ強調 Poisson)」レポートが表示されます。「パラメータ推定値の経路」、「元の説明変数に対する推定値」レポート、「効果の検定」レポートを見ると、1つの項において、その推定値がゼロに縮小されています。また、パラメータ推定値のレポートの最終行に表示されている「ゼロ強調」パラメータは高度に有意です。つまり、「釣った魚」におけるゼロ度数は、通常のPoisson分布よりも多く出現しているようです。
図7.6 「元の説明変数に対する推定値」レポート
「効果の検定」レポートからは、「生き餌」・「釣竿の本数」・「釣竿の本数*キャンプをした?」・「釣竿の本数*子供」の4つの項が、有意水準5%において有意であることがわかります。
11. 「弾性ネット (検証法: 検証列, 分布: ゼロ強調 Poisson)」の赤い三角ボタンをクリックし、[プロファイル]>[プロファイル]を選択します。
12. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度関数]を選択します。
「釣った魚」の数の最大化を目標とする満足度関数が、応答に適用されます。満足度関数については、『プロファイル機能』の満足度プロファイルと最適化を参照してください。
13. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度の最大化]を選択します。
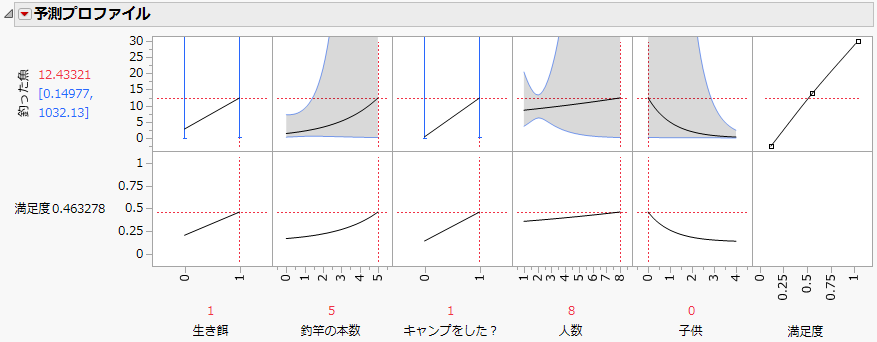
図7.7 釣った魚の数を最大にしたときの予測プロファイル
設定を変えながら、有意な要因である「生き餌」・「釣竿の本数」・「釣竿の本数*キャンプをした?」・「釣竿の本数*子供」の影響を確認できます。たとえば、「生き餌」を使うと、より多くの魚が釣れています。そして、「キャンプをした」方が、また持参した釣竿が多い方がより多くの魚を釣っています。
14. 「弾性ネット (検証法: 検証列, 分布: ゼロ強調 Poisson)」レポートの赤い三角ボタンをクリックし、[列の保存]>[予測式の保存]と[列の保存]>[分散計算式の保存]を選択します。
データテーブルに、「釣った魚 予測式」と「分散 釣った魚」という2列が追加されます。
15. 計算式を確認するには、データテーブルでどちらかの列の見出しを右クリックし、[計算式]を選択します。または、「列」パネルの列名の右側にある+記号をクリックします。これらの2つの計算式には、ゼロ強調パラメータの推定値0.781522155が使用されています。