隠れ層の構造
「ニューラル」プラットフォームでは、1層または2層のニューラルネットワークをあてはめることができます。第1層のノード数を増やすか、第2層を追加すると、ニューラルネットワークの柔軟性が増します。各層に含めるノードの数には制限がありません。第2層のノードは、X変数の関数です。第1層のノードは、第2層のノードの関数です。Y変数は、第1層のノードの関数です。
メモ: JMPの標準バージョンでは、活性化関数としてTanH関数しか使用できず、また、隠れ層が1つのニューラルネットワークしかあてはめられません。
注意: ブースティングは、2層のニューラルネットワークには使用できません。第2層に0以外の値を指定し、さらにブースティングも指定すると、第2層は無視されます。
隠れ層の各ノードで使われる関数を、「活性化関数」といいます。活性化関数は、X変数の線形結合を変換したものです。以下の活性化関数を使用できます。
TanH
TanH関数(双曲正接関数)は、シグモイド関数です。TanH関数は、結果が-1~1の範囲に収まるように尺度化されたロジスティック関数です。TanH関数は次式で表されます。
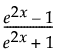
xはX変数の線形結合です。
線形
恒等関数です。X変数の線形結合を、そのまま変換しないで用います。
この線形関数は、非線形関数と併用するのが普通です。線形関数を第2層の活性化関数とし、非線形関数を第1層の活性化関数として配置すると、X変数の次元を減らしてからY変数の非線形モデルを作成できます。
線形の活性化関数だけを使用すると、Y変数が連続尺度の場合には、Y変数に対するモデルは、X変数の線形結合で表されるので、通常の線形回帰モデルとなります。また、Y変数が順序尺度や名義尺度の場合には、通常のロジスティック回帰モデルとなります。
Gauss
Gauss関数です。動径基底関数ネットワークにする場合、または応答曲面の形状がGauss分布(正規分布)の密度関数である場合にこのオプションを使用します。Gauss関数は次式で表されます。
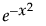
xはX変数の線形結合です。