独立二標本Poisson平均の検出力
「独立二標本Poisson平均の検出力エクスプローラ」では、独立な2つの標本のPoisson平均に対する仮説検定での標本サイズや検出力を計算できます。[実験計画(DOE)]>[標本サイズエクスプローラ]>[検出力] >[独立二標本Poisson平均の検出力]を選択します。 ばらつき・標本サイズ・検出力・有意水準・検出したい比におけるトレードオフの関係を調べることができます。ここでの仮説検定は、次のような帰無仮説に対するものです。
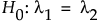
両側検定における対立仮説は、次のとおりです。
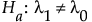
片側検定における対立仮説は次のとおりです。
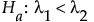 もしくは
もしくは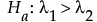
この式で、l1およびl2は、各群のユニットあたり度数です。
「独立二標本Poisson平均の検出力エクスプローラ」の設定
ラジオボタン・テキストボックス・メニューによって、実験や調査の仮定(仮説検定に用いる前提)を設定します。それらの設定を変更すると、プロファイルが更新されます。プロファイル上で十字をドラッグすることでも、設定を変更できます。
検定の種類
仮説検定が片側なのか両側なのかを指定します。
設定
アルファ
第1種の誤りの確率(帰無仮説が正しい場合に、その帰無仮説を誤って棄却する確率)です。この値は、一般には、「有意水準」や「α水準」などと呼ばれています。デフォルトの有意水準は0.05です。
帰無仮説での群間比
帰無仮説における、「群1のユニットあたり度数」に対する「群2のユニットあたり度数」の比。
「独立二標本Poisson平均の検出力エクスプローラ」のプロファイル
プロファイルは、標本サイズが検出力の計算にどのような影響を与えるかを示します。
全体の標本サイズ
実験に必要な全体の標本サイズ(実験回数・実験ユニット数・試料の個数・観測数など)。全体の標本サイズを固定するには、[ロック]を選択します。
解を求めたい対象:
ここでは何を求めたいかを指定します。標本サイズ、検出したい比、群1のユニットあたり度数のいずれかを選択してください。
検出力
帰無仮説が正しくないときに、その帰無仮説を正しく棄却できる確率。その他の設定が同じである場合、標本サイズが大きくなるほど、検出力は増加します。
群1の標本サイズ
実験において群1に必要なユニットの数を指定します。
群2の標本サイズ
実験において群2に必要なユニットの数を指定します。
対立仮説における群間比
対立仮説における、「群1のユニットあたり度数」に対する「群2のユニットあたり度数」の比を指定します。
群1のユニットあたり度数
群1のユニットあたり度数を指定します。群2のユニットあたり度数は、群1のユニットあたり度数と検出したい比から計算されます。
「独立二標本Poisson平均の検出力エクスプローラ」のオプション
「エクスプローラ」の赤い三角ボタンのメニューとレポートのボタンを使って、以下のオプションが使用できます。
シミュレーションデータ
データテーブルが開き、エクスプローラでの設定に基づいてシミュレートしたデータが表示されます。応答列の計算式は、乱数を生成するための計算式となっており、指定された設定に対応したものになっています。
収集用データテーブルの作成
データの収集に使える新しいデータテーブルが作成されます。データテーブルには、データを分析するためのスクリプトも含まれています。
設定の保存
現在の設定が「設定の保存」の表に保存されます。複数の異なる計画を保存して、比較することができます。「標本サイズエクスプローラの「設定の保存」」を参照してください。
ヘルプ
JMPヘルプを開きます。
「独立二標本Poisson平均の検出力エクスプローラ」の統計的詳細
独立二標本Poisson平均の検出力エクスプローラは、Poisson比の漸近的な正規分布に基づいて計算を行います。
下片側対立仮説の場合:
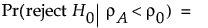
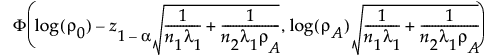
上片側対立仮説の場合:
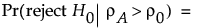
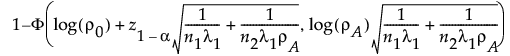
両側対立仮説の場合:
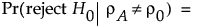
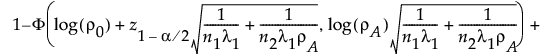
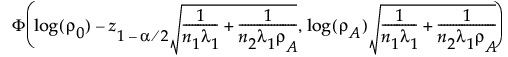
ここで
aは、有意水準。
n1およびn2は、各群の標本サイズ。
r0は、帰無仮説における、2群の「ユニットあたり度数」の比。
rAは、対立仮説における、2群の「ユニットあたり度数」の比。
l1は、帰無仮説における群1の比。
z1-αは、正規分布の(1 - a)分位点。
F(x)は、正規分布の累積分布関数。