連続型確率関数
Beta Density(x, alpha, beta, <theta=0>, <sigma=1>)
説明
ベータ分布のxにおける密度を戻す。密度関数は、次式のとおりです。
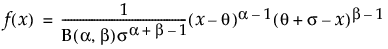
この式で、B(·)はベータ関数です。
引数
x
密度を求めたい分位点。xは、thetaとtheta + sigmaの間にある分位点。
alpha, beta
形状パラメータaおよびb。両者とも正の値。
theta
（オプション）閾値パラメータq。デフォルト値は0。
sigma
（オプション）尺度パラメータs。正の値。デフォルト値は1。
メモ
ベータ分布は、分位点xの定義域が無限であるような正規分布やガンマ分布とは異なり、限定された区間に対してだけ正の密度を持ちます。ベータ分布は、割合のような、範囲が0から1までに制限されている確率変数をモデル化する場合に役立ちます。
Beta Distribution(x, alpha, beta, <theta=0>, <sigma=1>)
説明
ベータ分布のxの下側累積確率を戻す。パラメータはBeta Density()関数と同じです。
引数
x
下側累積確率を求めたい分位点。xは、thetaとtheta + sigmaの間にある分位点。
alpha, beta
形状パラメータaおよびb。両者とも正の値。
theta
（オプション）閾値パラメータq。デフォルト値は0。
sigma
（オプション）尺度パラメータs。正の値。デフォルト値は1。
Beta Quantile(p, alpha, beta, <theta=0>, <sigma=1>)
説明
指定されたパラメータをもつベータ分布の下側累積確率pに対する分位点を戻す。分位点は、閉じた解析的な解としては求めることができません。
引数
p
下側累積確率。pは0～1の間でなければなりません。
alpha, beta
形状パラメータaおよびb。両者とも正の値。
theta
（オプション）閾値パラメータq。デフォルト値は0。
sigma
（オプション）尺度パラメータs。正の値。デフォルト値は1。
Cauchy Density(q, <center=0>, <scale=1>)
説明
Cauchy分布のqにおける密度を戻す。密度関数は、次式のとおりです。
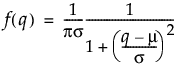
引数
q
密度を求めたい分位点。
center
（オプション）位置パラメータm。デフォルト値は0。
scale
（オプション）尺度パラメータs。正の値。デフォルト値は1。
Cauchy Distribution(q, <center=0>, <scale=1>)
説明
Cauchy分布に従う変数がq以下になる確率を戻す。累積分布関数は、次式のとおりです。
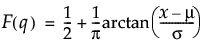
引数
q
下側累積確率を求めたい分位点。
center
（オプション）位置パラメータm。デフォルト値は0。
scale
（オプション）尺度パラメータs。正の値。デフォルト値は1。
Cauchy Quantile(p, <center=0>, <scale=1>)
説明
Cauchy分布のpに対する分位点を戻す。この分位点は、Cauchy分布の下側累積確率がpとなる分位点です。分位点関数は、次式のとおりです。
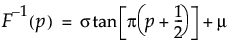
引数
p
下側累積確率。pは0～1の間でなければなりません。
center
（オプション）位置パラメータm。デフォルト値は0。
scale
（オプション）尺度パラメータs。正の値。デフォルト値は1。
ChiSquare Density(q, df, <nc=0>)
説明
カイ2乗分布のqにおける密度を戻す。密度関数は、次式のとおりです。
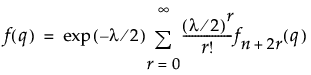
この式で、fn+2r(q) は、自由度がn+2rのカイ2乗分布の密度です。
引数
q
密度を求めたい分位点。qは0以上でなければなりません。
df
自由度n。正の値。
nc
（オプション）非心度パラメータl。負でない値。デフォルト値は0。
ChiSquare Distribution(q, df, <nc=0>)
説明
自由度をdf、オプションの非心度パラメータをncとしたカイ2乗分布の、分位点xにおける累積分布関数の値を戻す。累積分布関数は、次式のとおりです。
,
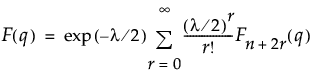この式で、Fn+2r(q)は、自由度がn+2rのカイ2乗分布の累積分布です。
引数
q
下側累積確率を求めたい分位点。qは0以上でなければなりません。
df
自由度n。正の値。
nc
（オプション）非心度パラメータl。負でない値。デフォルト値は0。
ChiSquare Log CDistribution(x, df, <nc=0>)
説明
(1 - value)の対数を戻す。ここで、valueは、自由度をdf、非心度パラメータをncとしたカイ2乗分布のxにおける下側累積確率。
ChiSquare Log Density(x, df, <nc=0>)
説明
自由度をdf、非心度パラメータをncとしたカイ2乗分布のxにおける下側累積確率の対数を戻す。
ChiSquare Log Distribution(x, df, <nc=0>)
説明
自由度をdf、非心度パラメータをncとしたカイ2乗分布のxにおける累積分布関数の値の対数を戻す。
ChiSquare Noncentrality(x, df, prob)
説明
以下の式を満たすカイ2乗分布の非心度パラメータncを戻す。
prob = ChiSquare Distribution(x, df, nc)
引数
x
下側累積確率を求めたい分位点。
df
自由度 n 。正の値。
prob
下側累積確率。probは0～1の間でなければなりません。
ChiSquare Quantile(p, df, <nc=0>)
説明
自由度をdf、オプションの非心度パラメータをncとしたカイ2乗分布の、下側累積確率pに対する分位点を戻す。分位点は、閉じた解析的な解としては求めることができません。
引数
p
下側累積確率。pは0～1の間でなければなりません。
df
自由度n。正の値。
nc
（オプション）非心度パラメータl。負でない値。デフォルト値は0。
Dunnett P Value(q, nTrt, dfe, <lambdaVec=.>)
説明
Dunnettの多重比較検定のp値を戻す。
引数
q
検定統計量の数値。
nTrt
対照群と比較する処置群の数。
dfe
誤差の自由度。
lambdaVec
相関構造を表すパラメータのベクトル。lambdaVecが欠測値（.）の場合、ベクトルのすべての要素は、1/Sqrt(2)に設定されます。
Dunnett Quantile(1-alpha, nTrt, dfe, <lambdaVec=.>)
説明
Dunnettの多重比較検定で使われる分位点を戻す。
引数
1-alpha
信頼水準を示す数値。
nTrt
対照群と比較する処置群の数。
dfe
誤差の自由度。
lambdaVec
相関構造を表すパラメータのベクトル。lambdaVecが欠測値（.）の場合、ベクトルのすべての要素は、1/Sqrt(2)に設定されます。
Exp Density(x, <theta=1>)
Exponential Density(x, <theta=1>)
説明
指数分布のxにおける密度を戻す。密度関数は、次式のとおりです。
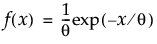
引数
x
密度を求めたい分位点。xは0以上でなければなりません。
theta
（オプション）尺度パラメータq。正の値。デフォルト値は1。
Exp Distribution(x, <theta=1>)
Exponential Distribution(x, <theta=1>)
説明
指数分布に従う確率変数がx以下になる確率を戻す。累積分布関数は、次式のとおりです。
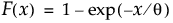
引数
x
下側累積確率を求めたい分位点。xは0以上でなければなりません。
theta
（オプション）尺度パラメータq。正の値。デフォルト値は1。
Exp Quantile(p, <theta=1>)
Exp Quantile(p, <theta=1>)
説明
尺度パラメータthetaを持つ指数分布の下側累積確率がpとなる分位点を戻す。分位点関数は、次式のとおりです。
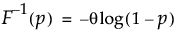
引数
p
下側累積確率。pは0～1の間でなければなりません。
theta
（オプション）尺度パラメータq。正の値。デフォルト値は1。
F Density(x, dfnum, dfden, <nc=0>)
説明
分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布のxにおける密度を戻す。
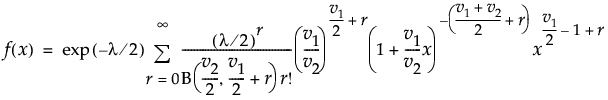
この式で、B(·)はベータ関数です。
引数
x
密度を求めたい分位点。xは正の値でなければなりません。
dfnum
F分布の分子に使用されるカイ2乗分布の自由度、v1。dfnumは、0より大きくなければなりません。
dfden
F分布の分母に使用されるカイ2乗分布の自由度、v2。dfdenは、0より大きくなければなりません。
nc
（オプション）非心度パラメータl。負でない値。デフォルト値は0。
F Distribution(x, dfnum, dfden, <nc=0>)
説明
分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布のxにおける下側累積確率を戻す。
F Log CDistribution(x, dfnum, dfden, <nc=0>)
説明
(1 - value)の対数を戻す。ここで、valueは、分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布のxにおける下側累積確率。
F Log Density(x, dfnum, dfden, <nc=0>)
説明
分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布のxにおける確率密度関数の値の対数を戻す。
F Log Distribution(x, dfnum, dfden, <nc=0>)
説明
分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布のxにおける累積分布関数の値の対数を戻す。
F Noncentrality(x, dfnum, dfden, prob)
説明
以下の式を満たすF分布の非心度パラメータnを戻す。
prob = F Distribution(x, dfnum, dfden, nc)
次も参照
F Distribution(x, dfnum, dfden, <nc=0>)
F Power(alpha, dfh, dfm, d, n)
説明
与えられた引数から算出されるF検定やt検定の検出力を戻す。
引数
alpha
検定の有意水準。alphaは、0～1の間でなければなりません。
dfh
仮説の自由度。dfhは、0より大きくなければなりません。
dfm
モデル全体の自由度。dfmは、0より大きくなければなりません。
d
効果の大きさの2乗。D2/s2と定義される。この式で、s2は誤差分散、D2は次のように定義されます。
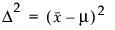1標本のt検定
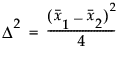2標本のt検定
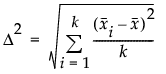k標本のF検定
n
観測（オブザベーション）の合計個数。nは、dfmより大きくなければなりません。
F Quantile(x, dfnum, dfden, <nc=0>)
説明
分子の自由度をdfnum、分母の自由度をdfden、オプションの非心度パラメータをncとしたF分布の下側累積確率pに対する分位点を戻す。
F Sample Size(alpha, dfh, dfm, d, power)
説明
与えられた引数から算出されるF検定やt検定の標本サイズを戻す。
引数
alpha
検定の有意水準。alphaは、0～1の間でなければなりません。
dfh
仮説の自由度。dfhは、0より大きくなければなりません。
dfm
モデル全体の自由度。dfmは、0より大きくなければなりません。
d
効果の大きさの2乗。D2/s2と定義される。この式で、s2は誤差分散、D2は次のように定義されます。
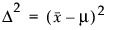1標本のt検定
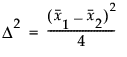2標本のt検定
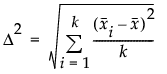k標本のF検定
power
検定の検出力。
Frechet Density(x, mu, sigma)
説明
Fréchet分布のxにおける密度を戻す。密度関数は、次式のとおりです。
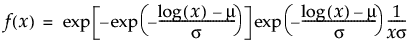
引数
x
密度を求めたい分位点。xは正の値でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Frechet Distribution(x, mu, sigma)
説明
Fréchet分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
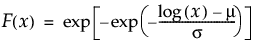
引数
x
下側累積確率を求めたい分位点。xは正の値でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Frechet Quantile(p, mu, sigma)
説明
位置mu、尺度sigmaのFréchet分布の、下側累積確率pに対する分位点を戻す。分位点関数は、次式のとおりです。
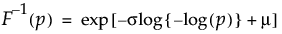
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Gamma Density(x, <alpha=1>, <scale=1>, <threshold=0>)
説明
ガンマ分布のxにおける密度を戻す。密度関数は、次式のとおりです。
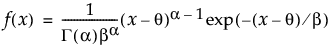
引数
x
密度を求めたい分位点。xはqより大きくなければなりません。
alpha
（オプション）形状パラメータa。正の値。デフォルト値は1。
scale
（オプション）尺度パラメータb。正の値。デフォルト値は1。
threshold
（オプション）閾値パラメータq。デフォルト値は0。
Gamma Distribution(x, <alpha=1>, <scale=1>, <threshold=0>)
IGamma(x, <alpha=1, scale=1, threshold=0>)
説明
形状パラメータ（alpha）、尺度パラメータ（scale）、閾値パラメータ（threshold）を持つガンマ分布の、分位点xにおける累積分布関数の値を戻す。
Gamma Log CDistribution(x, <alpha=1>, <scale=1>, <threshold=0>)
説明
計算できる範囲がはるかに大きいことを除けば、Log(1 - Gamma Distribution(x, alpha))と同じ。
Gamma Log Density(x, <alpha=1>, <scale=1>, <threshold=0>)
説明
計算できる範囲がはるかに大きいことを除けば、Log(GammaDensity(x, alpha))と同じ。
Gamma Log Distribution(x, <alpha=1>, <scale=1>, <threshold=0>)
説明
計算できる範囲がはるかに大きいことを除けば、Log(Gamma Distribution(x, alpha))と同じ。
Gamma Quantile(p, <alpha=1>, <scale=1>, threshold>)
説明
形状パラメータ（alpha）、尺度パラメータ（scale）、閾値（threshold）を持つガンマ分布の、下側累積確率pに対する分位点を戻す。
GenGamma Density(x, mu, sigma, lambda)
説明
拡張一般化ガンマ分布のxにおける密度を戻す。密度関数は、次式のとおりです。
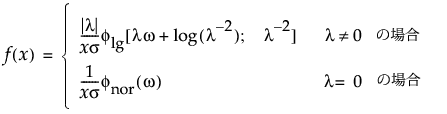
この式で、w = [log(x) – m]/s。次の式は、0より大きい形状パラメータkを持つ標準化した対数ガンマ分布の確率密度関数です。
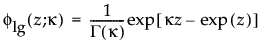
fnor(·)は、標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。xは正の値でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
GenGamma Distribution(x, mu, sigma, lambda)
説明
拡張一般化ガンマ分布の下側累積確率を戻す。累積分布関数は、次式のとおりです。
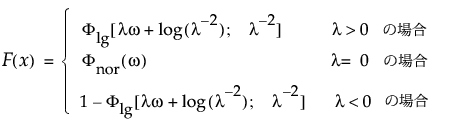
この式で、w = [log(x) – m]/s。次の式は、0より大きい形状パラメータkを持つ標準化した対数ガンマ分布の累積分布関数です。
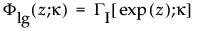
この式で、GI[·]は、不完全ガンマ関数を表します。Fnor(·)は、標準正規分布の累積分布関数です。
引数
x
下側累積確率を求めたい分位点。xは正の値でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
GenGamma Quantile(p, mu, sigma, lambda)
説明
パラメータmu、sigma、lambdaの拡張一般化ガンマ分布の下側累積確率がpとなる分位点を戻す。分位点は、閉じた解析的な解としては求めることができません。
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
GLog Density(x, mu, sigma, lambda)
説明
一般化対数分布のxにおける密度を戻す。密度関数は、次式のとおりです。
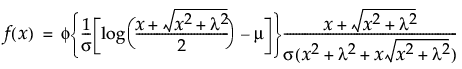
上の式で、f(·)は標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。正の値。
メモ
この分布は、パラメータlambdaが0の場合、Lognormal(m, s)の対数正規分布になります。
GLog Distribution(x, mu, sigma, lambda)
説明
一般化対数分布の累積分布関数。一般化対数分布に従う確率変数がx以下になる確率を戻す。累積分布関数は、次式のとおりです。
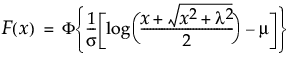
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
x
下側累積確率を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。正の値。
GLog Quantile(p, mu, sigma, lambda)
説明
一般化対数分布の下側累積確率がpとなる分位点を戻す。
IGamma()
Gamma Distribution(x, <alpha=1>, <scale=1>, <threshold=0>)を参照してください。
Johnson Sb Density(q, gamma, delta, theta, sigma)
説明
Johnson Sb分布のqにおける密度を戻す。密度関数は、次式のとおりです。
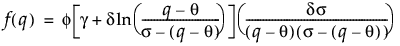
上の式で、f(·)は標準正規分布の確率密度関数です。
引数
q
密度を求めたい分位点。qは、theta～theta + sigmaの区間内でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Johnson Sb Distribution(q, gamma, delta, theta, sigma)
説明
Johnson Sb分布のqにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
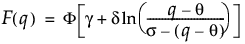
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
q
下側累積確率を求めたい分位点。qは、theta～theta + sigmaの区間内でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Johnson Sb Quantile(p, gamma, delta, theta, sigma)
説明
Johnson Sb分布の下側累積確率がpとなる分位点を戻す。
引数
p
下側累積確率。pは0～1の間でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Johnson Sl Density(x, gamma, delta, theta, sigma)
説明
Johnson Sl分布のxにおける密度を戻す。密度関数は、次式のとおりです。
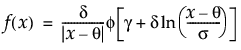
上の式で、f(·)は標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。xは、sigmaが1のときはthetaより大きい値、sigmaが-1のときはthetaより小さい値でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
分布が正の方向に歪むか、負の方向に歪むかを示すパラメータs。sigmaは、+1（正の方向）または-1（負の方向）のどちらかをとります。
Johnson Sl Distribution(q, gamma, delta, theta, sigma)
説明
Johnson Sl分布のqにおける下側累積確率を戻す。
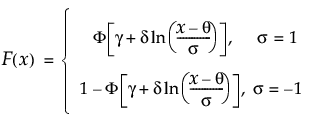
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
q
下側累積確率を求めたい分位点。qは、sigmaが1のときはthetaより大きい値、sigmaが-1のときはthetaより小さい値でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
分布が正の方向に歪むか、負の方向に歪むかを定義するパラメータs。Sigmaは、+1（正の方向）または-1（負の方向）のどちらかをとります。
Johnson Sl Quantile(p, gamma, delta, theta, sigma)
説明
Johnson Sl分布の下側累積確率がpとなる分位点を戻す。
引数
p
下側累積確率。pは0～1の間でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
分布が正の方向に歪むか、負の方向に歪むかを定義するパラメータs。Sigmaは、+1（正の方向）または-1（負の方向）のどちらかをとります。
Johnson Su Density(x, gamma, delta, theta, sigma)
説明
Johnson Su分布のxにおける密度を戻す。密度関数は、次式のとおりです。
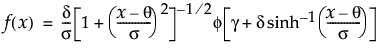
上の式で、f(·)は標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Johnson Su Distribution(q, gamma, delta, theta, sigma)
説明
Johnson Su分布のqにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
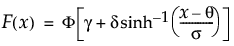
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
q
下側累積確率を求めたい分位点。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Johnson Su Quantile(p, gamma, delta, theta, sigma)
説明
Johnson Su分布の下側累積確率がpとなる分位点を戻す。
引数
p
下側累積確率。pは0～1の間でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
LEV Density(x, mu, sigma)
説明
位置mu、尺度sigmaの最大極値分布のxにおける密度を戻す。密度関数は、次式のとおりです。
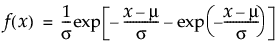
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
LEV Distribution(x, mu, sigma)
説明
位置mu、尺度sigmaの最大極値分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
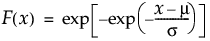
引数
x
下側累積確率を求めたい分位点。xは、sigmaより大きくなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
LEV Quantile(p, mu, sigma)
説明
位置mu、尺度sigmaの最大極値分布の下側累積確率がpとなる分位点を戻す。分位点関数は、次式のとおりです。
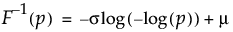
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
LogGenGamma Density(x, mu, sigma, lambda)
説明
パラメータがmu、sigma、lambdaの対数一般化ガンマ確率分布のxにおける密度を戻す。密度関数は、次式のとおりです。
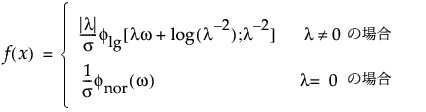
この式で、 w = [x – m]/sです。次の式は、0より大きい形状パラメータkを持つ対数ガンマ分布の確率密度関数です。
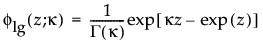
fnor(·)は、標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
LogGenGamma Distribution(x, mu, sigma, lambda)
説明
パラメータがmu、sigma、lambdaの対数一般化ガンマ分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
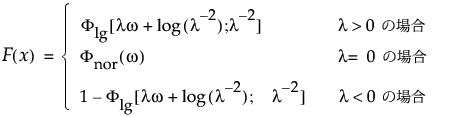
この式で、 w = [x – m]/sです。次の式は、0より大きい形状パラメータkを持つ対数ガンマ分布の累積分布関数です。
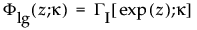
この式で、GI[·]は、不完全ガンマ関数を表します。Fnor(·)は、標準正規分布の累積分布関数です。
引数
x
下側累積確率を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
LogGenGamma Quantile(p, mu, sigma, lambda)
説明
対数一般化ガンマ分布の第p分位点を戻す。
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
lambda
形状パラメータl。
Logistic Density(x, mu, sigma)
説明
位置mu、尺度sigmaのロジスティック分布のxにおける密度を戻す。密度関数は、次式のとおりです。
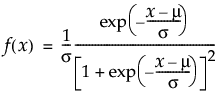
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Logistic Distribution(x, mu, sigma)
説明
位置mu、尺度sigmaのロジスティック分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
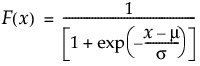
引数
x
下側累積確率を求めたい分位点。xは、sより大きくなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Logistic Quantile(p, mu, sigma)
説明
位置mu、尺度sigmaのロジスティック分布の下側累積確率がpとなる分位点を戻す。分位点関数は、
次式のとおりです。
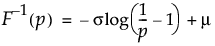
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Loglogistic Density(x, mu, sigma)
説明
位置mu、尺度sigmaの対数ロジスティック分布のxにおける密度を戻す。密度関数は、次式のとおりです。
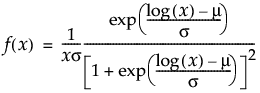
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Loglogistic Distribution(x, mu, sigma)
説明
位置mu、尺度sigmaの対数ロジスティック分布のxにおける下側累積確率を戻す。累積分布関数は、
次式のとおりです。
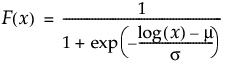
引数
x
下側累積確率を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Loglogistic Quantile(p, mu, sigma)
説明
位置mu、尺度sigmaの対数ロジスティック分布の下側累積確率がpとなる分位点を戻す。分位点関数は、次式のとおりです。
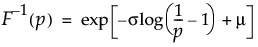
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Lognormal Density(x, mu, sigma)
説明
位置mu、尺度sigmaの対数正規分布のxにおける密度を戻す。密度関数は、次式のとおりです。
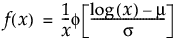
上の式で、f(·)は標準正規分布の確率密度関数です。
引数
x
密度を求めたい分位点。xは0以上でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Lognormal Distribution(x, mu, sigma)
説明
位置mu、尺度sigmaの対数正規分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
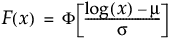
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
x
密度を求めたい分位点。xは0以上でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
Lognormal Quantile(x, mu, sigma)
説明
位置mu、尺度sigmaの対数正規分布の下側累積確率がpとなる分位点を戻す。
Normal Biv Distribution(x, y, r, <mu1>, <s1>, <mu2>, <s2>)
説明
2変量正規分布に従う確率変数(X, Y)が(x, y)以下になる確率を計算する。ここで、Xの周辺分布は平均mu1、標準偏差s1、Yの周辺分布は平均mu2、標準偏差s2の正規分布に従っているとします。また、
2変量の相関関数はrとします。mu1、s1、mu2、s2が指定されていない場合、mu1=0、s1=1、mu2=0、s2=1の標準正規分布が使われます。
Normal Density(x, <mean=0>, <stddev=1>)
説明
平均（mean）、標準偏差（stddev）を持つ正規分布の、xにおける密度を戻す。密度関数は、次式のとおりです。
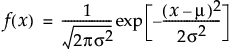
引数
x
密度を求めたい分位点。
mu
（オプション）位置パラメータm。デフォルト値は0。
sigma
（オプション）尺度パラメータs。正の値。デフォルト値は1。
メモ
正規分布は、西洋の教会にあるベルの形状をした、左右対称な分布です。
Normal Distribution(x, <mean=0>, <stddev=1>)
説明
平均（mean）、標準偏差（stddev）を持つ正規分布の、xにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
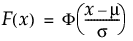
F(·)は標準正規分布の累積分布関数で、次のように定義されます。
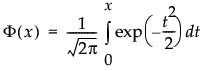
引数
x
密度を求めたい分位点。
mu
（オプション）位置パラメータm。デフォルト値は0。
sigma
（オプション）尺度パラメータs。正の値。デフォルト値は1。
Normal Log CDistribution(x, <mean=0>, <std dev=1>)
説明
正規分布の分位点xでの上側累積確率の対数を戻す。
Normal Log Density(x, <mean=0>, <stddev=1>)
説明
平均（mean）、標準偏差（stddev）を持つ正規分布の、分位点xにおける密度関数の値の対数を戻す。デフォルトの平均（mean）は0です。デフォルトの標準偏差（stddev）は1です。
Normal Log Distribution(x, <mean=0>, <std dev=1>)
説明
正規分布の分位点xでの累積分布関数の値の対数を戻す。
Normal Mixture Density(q, mean, stdev, probability)
説明
正規混合分布の密度関数。グループ平均mean、グループ標準偏差stdev、グループ確率probabilityのqにおける密度を戻す。mean、stdev、およびprobabilityはすべて同じサイズのベクトルです。
Normal Mixture Distribution(q, mean, stdev, probability)
説明
正規混合分布の確率関数。グループ平均mean、グループ標準偏差stdev、グループ確率probabilityの正規混合分布に従う確率変数がqよりも小さい確率を戻す。mean、stdev、およびprobabilityはすべて同じサイズのベクトルです。
Normal Mixture Quantile(p, mean, stdev, probability)
説明
正規混合分布の下側累積確率がpとなる分位点を戻す。mean、stdev、およびprobabilityはすべて同じサイズのベクトルです。
Normal Quantile(p, <mean=0>, <stddev=1>)
Probit(p, <mean=0>, <stddev=1>)
説明
平均（mean）、標準偏差（stddev）をもつ正規分布の下側累積確率がpとなる分位点を戻す。デフォルトの平均（mean）は0です。デフォルトの標準偏差（stddev）は1です。
Probit()
Normal Quantile(p, <mean=0>, <stddev=1>)を参照してください。
SEV Density(x, mu, sigma)
説明
位置mu、尺度sigmaの最小極値分布のxにおける密度を戻す。密度関数は、次式のとおりです。
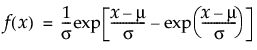
引数
x
密度を求めたい分位点。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
SEV Distribution(x, mu, sigma)
説明
位置mu、尺度sigmaの最小極値分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
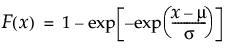
引数
x
下側累積確率を求めたい分位点。xは、sより大きくなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
SEV Quantile(p, mu, sigma)
説明
位置mu、尺度sigmaの最小極値分布の下側累積確率がpとなる分位点を戻す。分位点関数は、次式のとおりです。
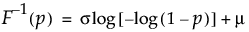
引数
p
下側累積確率。pは0～1の間でなければなりません。
mu
位置パラメータm。
sigma
尺度パラメータs。正の値。
SHASH Density(x, gamma, delta, theta, sigma)
説明
sinh-arcsinh（SHASH）分布のxにおける密度を戻す。密度関数は、次式のとおりです。
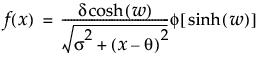
ここで、
f(·)は標準正規分布の確率密度関数です。
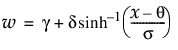
引数
x
密度を求めたい分位点。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
SHASH Distribution(x, gamma, delta, theta, sigma)
説明
sinh-arcsinh（SHASH）分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
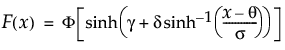
上の式で、F(·)は標準正規分布の累積分布関数です。
引数
x
下側累積確率を求めたい分位点。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
SHASH Quantile(p, gamma, delta, theta, sigma)
説明
sinh-arcsinh（SHASH）分布の下側累積確率がpとなる分位点を戻す。分布のパラメータは、gamma、delta、theta、sigmaです。
引数
p
下側累積確率。pは0～1の間でなければなりません。
gamma
形状パラメータg。
delta
形状パラメータd。正の値。
theta
位置パラメータq。
sigma
尺度パラメータs。正の値。
Students t Density()
t Density(x, df, <nc=0>)を参照してください。
Students t Distribution()
t Distribution(q, df, <nc=0>)を参照してください。
Students t Quantile()
t Quantile(p, df, <nc=0>)を参照してください。
t Density(x, df, <nc=0>)
Students t Density(x, df, <nc=0>)
説明
指定された自由度（df）をもつStudentのt分布のxにおける密度を戻す。密度関数は、次式のとおりです。
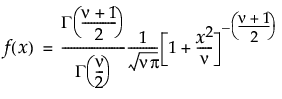
引数
x
密度を求めたい分位点。
df
自由度n。値は1以上でなければなりません。
nc
（オプション）非心度パラメータl。負でない値。デフォルト値は0。
t Distribution(q, df, <nc=0>)
Students t Distribution(q, df, <nc=0>)
説明
Studentのt分布の累積分布関数。Studentのt分布に従う確率変数がq以下になる確率を戻します。
ncのデフォルト値は0です。
t Log CDistribution(x, df, <nc=0>)
説明
t分布の分位点xでの上側累積確率の対数を戻す。
t Log Density(x, df, <nc=0>)
説明
t分布の分位点xでの密度関数の値の対数を戻す。
t Log Distribution(x, df, <nc=0>)
説明
t分布の分位点xでの累積分布関数の値の対数を戻す。
t Noncentrality(x, df, prob)
説明
以下の式を満たすt分布の非心度パラメータncを戻す。
prob = T Distribution(x, df, nc)
t Quantile(p, df, <nc=0>)
Students t Quantile(p, df, <nc=0>)
説明
Studentのt分布の分位点関数。指定された自由度（df）をもつStudentのt分布の、下側累積確率がpとなる分位点を戻す。ncのデフォルト値は0です。
Tukey HSD P Value(q, n, dfe)
説明
TukeyのHSD多重比較検定のp値を戻す。
引数
q
検定統計量。多重性の調整をされたTukey検定の棄却値であり、スチューデント化範囲の分位点を2の平方根で割った値です。
n
検定されるグループの数。
dfe
すべての標本から計算される誤差の自由度。
Tukey HSD Quantile(1-alpha, n, dfe)
説明
TukeyのHSD多重比較検定に使用される分位点を戻す。戻される分位点は、多重性の調整をされたTukey検定の棄却値であり、スチューデント化範囲の分位点を2の平方根で割った値です。
引数
1-alpha
信頼水準。
n
検定されるグループの数。
dfe
すべての標本から計算される誤差の自由度。
Weibull Density(x, shape, <scale=1>, <threshold=0>)
説明
Weibull分布のxにおける密度を戻す。密度関数は、次式のとおりです。
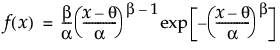
引数
x
密度を求めたい分位点。xは、thresholdより大きくなければなりません。
shape
形状パラメータb。正の値。
scale
（オプション）尺度パラメータa。正の値。デフォルト値は1。
threshold
（オプション）閾値パラメータq。デフォルト値は0。
Weibull Distribution(x, shape, <scale=1>, <threshold=0>)
説明
Weibull分布のxにおける下側累積確率を戻す。累積分布関数は、次式のとおりです。
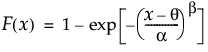
引数
x
密度を求めたい分位点。xは、thresholdより大きくなければなりません。
shape
形状パラメータb。正の値。
scale
（オプション）尺度パラメータa。正の値。デフォルト値は1。
threshold
（オプション）閾値パラメータq。デフォルト値は0。
Weibull Quantile(p, shape, <scale=1>, <threshold=0>)
説明
指定されたパラメータをもつWeibull分布の下側累積確率がpとなる分位点を戻す。分位点関数は、
次のように計算されます。
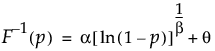
引数
p
下側累積確率。pは0～1の間でなければなりません。
shape
形状パラメータb。正の値。
scale
（オプション）尺度パラメータa。正の値。デフォルト値は1。
threshold
（オプション）閾値パラメータq。デフォルト値は0。