正準の詳細を表示
「判別分析」プラットフォームの「正準の詳細」レポートには、共変量とグループ変数Xの関係を示す検定が表示されます。レポートの下部に、関連する行列が表示されます。
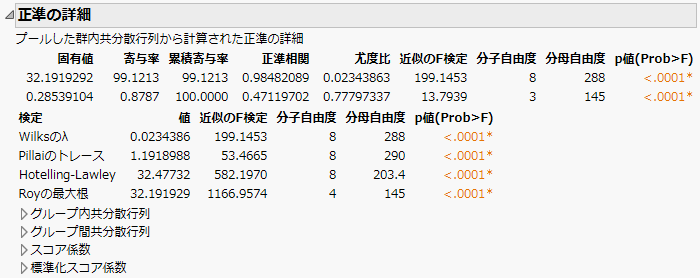
図5.11 「Iris.jmp」の正準の詳細
メモ: この正準分析で使用される共分散行列は、常にプールした群内共分散行列(プールしたグループ内共分散行列)です。どの判別法を選択したとしても、「正準の詳細」レポートでは、プールした群内共分散行列が常に使われます。そのため、「正準の詳細」レポートの統計量や検定は、すべての判別法で共通です。
統計量と検定
「正準の詳細」レポートには、固有値がリストされ、「固有値がゼロである」という帰無仮説に対する尤度比検定が表示されます。また、「正準相関がゼロである」という帰無仮説に対して、4つの検定が表示されます。
固有値
グループ間共分散行列(群間共分散行列)と、グループ内共分散行列(群内共分散行列)の逆行列を掛け合わせた行列の固有値。固有値は、大きい順に表示されます。固有値の大きさは、その次元における、判別で説明される分散の量を反映しています。
寄与率
固有値の合計に対する、該当の固有値が占める割合。
累積寄与率
寄与率の累積合計。
正準相関
カテゴリカル変数Xのグループと、共変量との間の正準相関。まず、Xのグループから、指示変数(ダミー変数)を作成します。そして、一方の変数の組を指示変数とし、もう一方の変数の組を共変量として、正準相関分析を行います。「正準相関」に表示されている値は、この正準相関分析における正準相関の値です。
尤度比
現在の次元以降の母正準相関がすべてゼロかどうかを調べる検定の尤度比統計量。この尤度比統計量は、現在の次元以降に関して、(1 - 正準相関2)を掛け合わせたものです。
検定
「共変量の平均はグループ間で等しい」という帰無仮説に対する検定で、WilksのΛ、Pillaiのトレース、Hotelling-Lawleyのトレース、およびRoyの最大根の4つが計算されます。多変量検定の統計的詳細および近似F検定の統計的詳細を参照してください。
近似のF検定
対応する検定のF値。一部の検定では、F値は近似値または上限値です。近似F検定の統計的詳細を参照してください。
分子自由度
対応する検定の分子自由度。
分母自由度
対応する検定の分母自由度。
p値(Prob>F)
対応する検定のp値。
行列
レポートの下部に、正準構造に関連する4つの行列が表示されます。行列を表示するには、それぞれの名前の横にある開閉アイコンをクリックしてください。また、非表示にするには、行列の名前をクリックしてください。
グループ内共分散行列
プールしたグループ内共分散行列(群内共分散行列)。
グループ間共分散行列
グループ間共分散行列(群間共分散行列)、SB。群間共分散行列の統計的詳細を参照してください。
スコア係数
生データから正準スコアを計算する際に使用する係数。この係数が、[正準オプション]>[正準スコアの保存]オプションに使用されます。これらの計算方法の詳細については、SAS Institute Inc.(2020b)の「CANDISC Procedure」章を参照してください。
標準化スコア係数
標準データから正準スコアを計算する際に使用する係数。この係数は、一般に、正準重み(canonical weight)と呼ばれています。これらの計算方法の詳細については、SAS Institute Inc.(2020b)の「CANDISC Procedure」章を参照してください。