多変量検定の統計的詳細

以下において、Eは残差交差積行列、Hはモデル交差積行列です。Eの対角要素は、各変数の残差平方和です。Hの対角要素は、各変数のモデル平方和です。判別分析に関する文献では、Eは、「within」の頭文字を取ってWと呼ばれることもあります。

多変量検定の結果に出力される検定統計量は、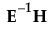の固有値lの関数になっています。次の一覧は、各検定統計量の計算方法をまとめたものです。

メモ: 応答に対する計画行列を指定すると、E行列とH行列の前からM′が、後ろからMが掛けられます。

• WilksのΛ

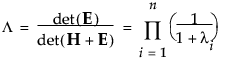
• Pillaiのトレース

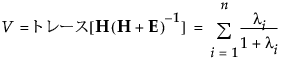
• Hotelling-Lawleyのトレース

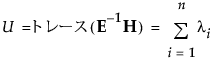
• Royの最大根

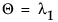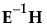= の最大固有値

EとHは次のように定義されます。

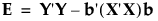
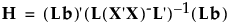
ここで、bはモデル係数の推定値を要素とするベクトル、A-は行列Aの一般化逆行列です。

モデル全体のL行列は、（切片に対する）ゼロの列に、モデルパラメータと同数の行と列を持つ単位行列を連結したものです。各効果のL行列は、モデル全体のL行列から、該当する行を抜き出したものです。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).