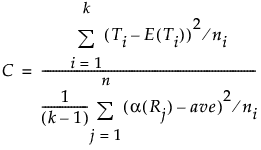ノンパラメトリックな検定の統計量の統計的詳細
この節では、「一元配置」プラットフォームのWilcoxon検定、メディアン検定、Van der Waerden検定、Friedmanの順位検定の統計量を求める式を紹介します。
表記
これらの順位検定はスコアに基づいています。以下の説明では、次の表記を使用するものとします。
j = 1,..., n
標本全体の観測値に対する通し番号。
i = 1,..., k
Xの水準。kは水準の総数。
n1, n2,..., nk
Xの第k水準における標本サイズ。
Rj
j番目の観測値の中間順位。中間順位は、同順位がない場合には、通常の順位です。同順位があった場合は、それらの同順位のものの順位の平均(中間値)です。
a
中間順位を変換する関数。各検定でスコアを定義するために使用します。
起動ウィンドウでブロック変数を指定した場合、次の表記が使用されます。
b = 1,..., B
ブロック変数の水準。Bはブロックの総数。
Rbi
ブロックb内における、第i観測値の中間順位。
関数aは、以下のようにスコアを定義します。
Wilcoxonのスコア
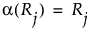
メディアンのスコア

メディアン(中央値)で同順位となる観測値の個数をntとし、nuをメディアンより大きい観測値の個数とすると、tは次のように求められます。
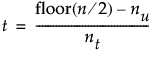
Van der Waerdenのスコア
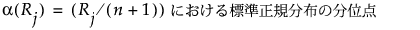
Friedmanの順位スコア
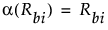
2標本の場合における正規近似
Xの水準が2水準の場合には、カイ2乗近似の統計量だけではなく、正規近似の統計量も計算されます。この節で使用される表記については、表記を参照してください。「2標本検定 (正規近似)」レポートに表示される統計量の定義は、以下のとおりです。
S
統計量Sは、観測値の個数が少ないほうの水準のa(Rj)を合計した値です。両水準における観測値の個数が等しい場合は、値の順序で並べて後になる水準を使用します。
Z
Zは次のように定義されます。
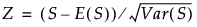
メモ: X変数が2水準である場合、Wilcoxon検定だけ、0.5の連続修正が「正規近似」のほうでは行われます(「カイ2乗近似」のほうは0.5の連続修正を行っていません)。(S - E(S))がゼロより大きい場合は、分子から0.5を引きます。(S - E(S))がゼロより小さい場合は、分子に0.5を足します。
E(S)
帰無仮説のもとでのSの期待値。観測値の個数が少ないほうの水準、または、両水準における観測値の個数が等しい場合は値の順序で並べて後になる水準の観測値の個数を、nlで表します。
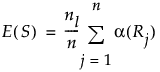
Var(S)
全観測値の平均スコアをaveとすると、Sの分散は次のように定義されます。
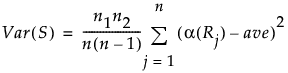
Friedmanの順位検定における、2標本の場合の正規近似
Friedmanの順位検定では、2標本の場合の正規近似の計算方法は、Sの分散を除き上記と同じです。Sの分散は、次のような式で計算されます。
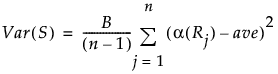
一元配置のカイ2乗近似
メモ: 通常の平均順位スコアに基づく順位検定は、2群の時は「Wilcxon検定」や「Mann-Whitney検定」と呼ばれ、3群以上の場合には「Kruskal-Wallis検定」と呼ばれています。
この節で使用される表記については、表記を参照してください。カイ2乗検定の統計量の計算には、次の値が使用されます。
Ti
Xのi番目の水準のスコアの合計。
E(Ti)
i番目の水準の合計スコアの期待値。水準間に差はないという帰無仮説のもとで、次のように定義されます。
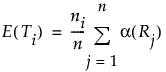
Var(T)
全観測値の平均スコアをaveとすると、Tの分散は次のように定義されます。
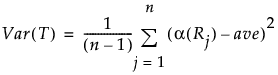
検定統計量は次の式で求められます。この検定統計量は、自由度がk – 1の漸近的なカイ2乗分布に従います。
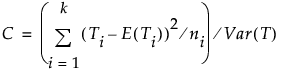
Friedmanの順位検定における、一元配置のカイ2乗近似
Friedmanの順位検定におけるカイ2乗検定の統計量は、次のような式で計算されます。