要約統計量の統計的詳細

ここでは、一変量の分布の「要約統計量」レポートに表示される個々の統計量について説明します。

平均

非欠測値の合計を、非欠測値の個数で割った値です。なお、［重み］や［度数］の列を起動ウィンドウで指定した場合は、次のように計算されます。

1. 各データ値に、対応する重みや度数を掛け合わせます。

2. 乗算後の値を合計し、それを、重みや度数の合計で割ります。

標準偏差

平均周りの分布の散らばりを示す指標です。通常はsで表されます。標準偏差は標本から計算された分散s2の平方根です。

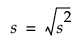
ここで、

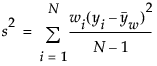
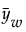= （重みつき）平均

平均の標準誤差

標準偏差sを、Nの平方根で割ったものです。ただし、［重み］や［度数］の列を起動ウィンドウで指定した場合は、重みや度数の合計の平方根で割ります。

歪度

平均周りの3次のモーメントを表す指標です。次式によって計算されます。

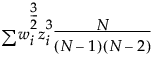この式で、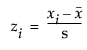

上の式で、wiは重みを表す係数（重み付けをしない場合は1）です。

尖度

平均周りの4次のモーメントを表す指標です。次式によって計算されます。

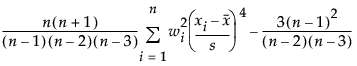
ここで、wiは重みです（重み付けをしない場合、すべての重みは1です）。この式によって求められた尖度は、正規分布の場合には0となります。このように正規分布のときに0となるように求められた尖度は、「過剰尖度」（excess kurtosis）と呼ばれることがあります。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).