「詳細」レポートの統計的詳細

「多重対応分析」プラットフォームでは、「詳細」レポートに特異値が表示されます。これらの特異値を求めるための特異値分解は、単純対応分析（simple correspondence analysis）で使用される特異値分解を拡張したものです。

単純対応分析においては、次式のような特異値分解が行われます。

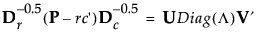
ここで

• Pは、合計度数（総和）で度数を割った値を要素とする行列

• rおよびcは、Pの行和と列和

• D行列は、rとcの値の対角行列

• Lは、特異値の列ベクトル

一方、多重対応分析においては、次式のような固有値分解が行われます。

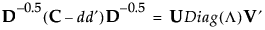
ここで

• Cは、Burt表

• dは、Cの列和から成る列ベクトル（Cは対称なので、dは行和でもあります）

• Dは、dの値から成る対角行列

多重対応分析での「詳細」レポートの「慣性」は、列ベクトルLです。また、「特異値」は、それら「慣性」の平方根です。列座標は、次のように計算されます。

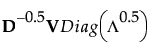
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).