多重対応分析

カテゴリカルな変数の水準間にある関係の特定

多重対応分析（Multiple Correspondence Analysis; MCA）は、複数のカテゴリカルな変数を分析対象とし、それらのカテゴリカルな変数の水準間にある関係を調べます。対応分析が2変数を分析するのに対し、多重対応分析は3変数以上を扱えます。多重対応分析は、「カテゴリカルな変数に対する主成分分析」と喩えることができます。他の多変量分析と同様に、次元を減らす手法であり、カテゴリカルな多変量データを2次元や3次元の空間で表します。

多重対応分析は、社会科学分野で広く利用されています。多重対応分析は、質問紙調査では、複数の質問における関係を調べるのに役立つでしょう。消費者調査では、潜在的な市場を探し出すのに使えるでしょう。

多重対応分析の詳細については、LeRoux and Rouanet（2010）を参照してください。

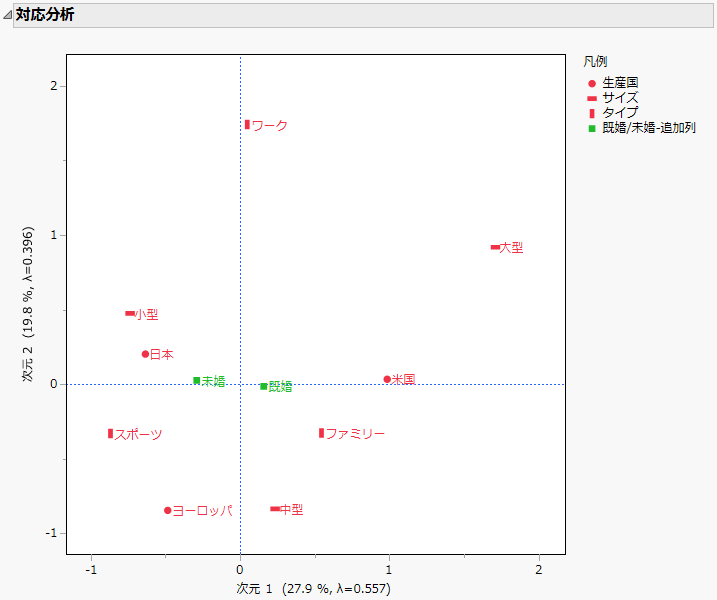
図7.1 多重対応分析 

目次

多重対応分析の例

「多重対応分析」プラットフォームの起動

「多重対応分析」レポート

「多重対応分析」プラットフォームのオプション

プロットの表示

詳細の表示

調整済み慣性の表示

座標の表示

要約統計量の表示

慣性への偏寄与率の表示

余弦2乗の表示

CochranのQ検定

クロス表

多重対応分析の別例

追加変数を使用した例

追加IDを使用した例

CochranのQ検定の例

「多重対応分析」プラットフォームの統計的詳細

「詳細」レポートの統計的詳細

調整済み慣性の統計的詳細

要約統計量の統計的詳細

CochranのQ検定の統計的詳細