最急降下法の統計的詳細

t-SNE法においてKullback-Leibler情報量を最小化するにあたっては、Barnes-Hut近似（van der Maaten, 2014）に基づき、最急降下法を使用しています。この方法では、次の表記法を使用しています。

X = {x1, x2, ..., xn} 元の高次元データ（n個のデータ点）

p = パープレキシティのパラメータ

T = 反復の回数

η = 学習率

tinflate = モーメンタム値が変化するまでの反復回数

a(t) = 反復tにおけるモーメンタム値。ここで、 t ≤ tinflateの場合はa(t) = 0.5、それ以外の場合はa(t) = 0.8

Y(t) = {y1, y2, ..., yn} 反復tにおける低次元空間に写像した座標

最急降下法の処理は、次のように行われます。

1. 高次元空間におけるペアの類似度pj|iを計算します。指定のパープレキシティpに基づき、σiを設定します。

2. pijを計算します。

3. 初期解Y(0) = {y1, y2, ..., yn}を設定します。これは、平均0、標準偏差10-4の正規分布から生成されます。

4. t = 1からTまで、次の処理を行います。

– 低次元マッピングにおけるペアの類似度qijを計算します。

– 次のようにコスト関数を計算します。

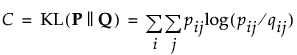
– Barnes-Hut近似を使って、次のように勾配関数を計算します。

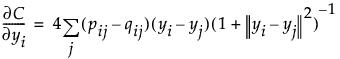
– 次のように解を更新します。

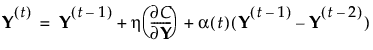
次の条件のいずれかが満たされた時点で、処理が停止します。

• iの勾配の最大値が、起動ウィンドウで指定した収束基準より小さい。

• 反復回数の最大値Tに達した。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).