ストレス関数の統計的詳細

「多次元尺度構成」プラットフォームでは、準Newton法を使ってストレス関数を最小化し、多次元尺度構成の座標を求めます。この方法では、あらかじめ指定した次元数での座標から予測される距離と実際の類似度との差が小さくなるように、座標が求められます。変換方法が順序尺度の場合は、単調回帰が使用されます。それ以外の変換方法では、最小2乗法による回帰が使用されます。

ストレスの定義では、次のような表記が使用されます。

• i、j - 対象に対する添え字

• dij - 対象iと対象jとの類似度の予測値

dij - 対象iと対象jとの間の相対距離の観測値

• f(drs) - 類似度を変換する関数

ストレス関数の計算式は次のとおりです。

Stress =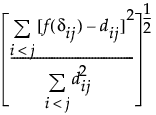

この測度は、Kruskalのストレス、タイプI、ストレスIとも呼ばれます。

より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).