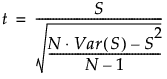Wilcoxonの符号付順位検定の統計的詳細
「一変量の分布」プラットフォームのWilcoxonの符号付順位検定は、1母集団、または対応のあるデータに対して用いることができ、分布が対称な場合には中央値に対する検定となります。対応のあるデータに対する検定は、それらの差に対する検定と等価です。この検定が中央値に対する検定となるには、母集団分布が対称でなければいけません。
Wilcoxonの符号付順位検定では、同順位も考慮されます。また、データ値にゼロがある場合は、Prattの方法で計算されます。Lehmann and D’Abrera(2006)、Pratt(1959)、およびCureton(1967)を参照してください。
1標本のWilcoxon符号付順位検定
• N個の観測値を、以下のように表すとします。
X1, X2, ..., XN
• Wilcoxon符号付き順位検定の帰無仮説は以下のようになります(なお、母集団分布が対称であるという前提のもとでは、中央値に対する検定になります)。
H0: Xの分布はmについて対称である
• 内部的な計算では、次式による観測値と仮説値mとの差が使われます。
Dj = Xj - m
対応のあるデータに対するWilcoxon符号付順位検定
対応のあるデータに対しても、次のような枠組みで、Wilcoxon符号付順位検定を適用できます。
• 2つの変数のそれぞれに、N個の観測値があるとします。
X1, X2, ..., XNおよびY1, Y2, ..., YN
• Wilcoxon符号付き順位検定の帰無仮説は以下のようになります(なお、母集団分布が対称であるという前提のもとでは、中央値に対する検定になります)。
H0: X - Yの分布は0について対称である
• 1標本の問題とするには、次のような計算式により観測値間の差を計算します。
Dj = Xj -Yj
Wilcoxon符号付順位検定の統計量
Wilcoxon符号付順位検定の統計量は、符号付き順位の合計に基づきます。符号付き順位は次のように定義されます。
• 差の絶対値⎟Dj⎟を、小さい値から順番に順位付けします。
• この時、差が0のものがあったとしても、順位付けにそれらの値も含めます。順位は1から始めます。
• また、差の絶対値に同じ値があった場合には、それらには平均順位(中間順位)を与えます。
以下において、差Djの順位(中間順位)をRjと記します。Djの符号付順位を、次のように定義します。
• 差Djが正の場合、符号付順位をRjとします。
• 差Djが0の場合、符号付順位を0とします。
• 差Djが負の場合、符号付順位を-Rjとします。
符号付順位の統計量は次のように計算されます。
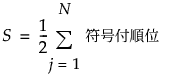
次のように定義します。
d0は、0と等しい観測値の個数。
R+は、正の符号付順位の合計。
このとき、次式が成立します。
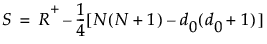
Wilcoxonの符号付順位検定のp値
N ≤ 20の場合は、正確なp値が計算されます。
N > 20の場合は、以下のように、Studentのt分布に近似して計算されます。同順位のペアに対して、修正が行われることに注意してください。Iman(1974)およびLehmann and D’Abrera(2006)を参照してください。
帰無仮説のもとでは、Sの平均はゼロです。Sの分散は次式により計算されます。
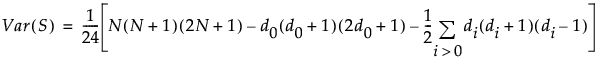
Var(S)の計算式の最後の和は、同順位のペアに対する修正です。i > 0に対するdiは、符号付順位が0以外で、かつ、符号付順位が同じグループに属するデータの個数を示します(符号付順位に同順位がまったくなければ、すべてがdi = 1となるので、この項は0となります)。
次式で求められた統計量tが、自由度N - 1のt分布で近似されます。