許容区間の統計的詳細
ここでは、「一変量の分布」プラットフォームにおける片側許容区間と両側許容区間の統計的詳細について説明します。
正規分布に基づく許容区間
片側許容区間
許容区間は、片側区間の場合、次式によって計算されます。
下側の場合=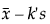 
上側の場合=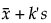 
ここで、
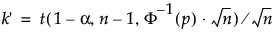
sは、標準偏差。
tは、非心t分布の分位点です。
F-1は、標準正規分布の分位点です。
両側許容区間
両側許容区間は、次の式で計算されます。
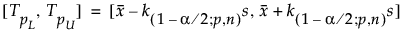
上の式で、sは標準偏差、k(1-a/2; p,n)は定数です。
kは、許容区間内に母集団の観測値が収まる割合に基づき計算されます。この割合は、次のように定義されます（Tamhane and Dunlop（2000））。
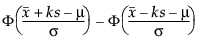
Fは標準正規分布の累積分布関数を表します。
そのため、kは次式を解くことにより計算されます。
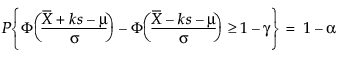
1-gが、母集団の観測値のうち、許容区間に含まれるものの割合となります。
正規分布に基づく許容区間の詳細については、Meeker et al.の表J.1a、J.1b、J.6a、J.6b（2017）を参照してください。
ノンパラメトリックな許容区間
下方片側の許容限界
信頼水準100(1 - a)%の下方片側許容限界（標本サイズnの標本分布において割合b以上のデータを含むもの）は、順序統計量x(l)です。この順位lは、次のように計算されます。
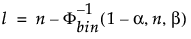
ここで、F-1bin(1-a, n, b)は、試行n回、成功確率bの二項分布の第(1 - a)分位点です。
実際の信頼水準は、Fbin(n-l, n, b)で計算されます。ここで、Fbin(x, n, b)は、試行n回、成功確率bの二項分布において、確率変数がx以下になる確率です。
なお、分布によらない下方片側許容限界を計算するには、標本サイズがnが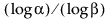
以上であることが前提となります。
上方片側の許容区間
信頼水準100(1 - a)%である上方片側許容限界（標本サイズnの標本分布において割合b以上のデータを含むもの）は、順序統計量x(u)です。この順位uは、次のように計算されます。
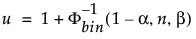
ここで、F-1bin(1-a, n, b)は、試行n回、成功確率bの二項分布の第(1 - a)分位点です。
実際の信頼水準は、Fbin(u-1, n, b)で計算されます。ここで、Fbin(x, n, b)は、試行n回、成功確率bの二項分布において、確率変数がx以下になる確率です。
なお、分布によらない上方片側許容限界を計算するには、標本サイズnが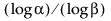
以上であることが前提となります。
両側許容区間
信頼水準100(1 - a)%の両側許容区間（標本サイズnの標本分布において割合b以上のデータを含むもの）は、次のように計算されます。
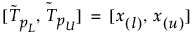
ここで、x(i)はi番目の順序統計量で、lとuは次のように計算されます。
n = n - F-1bin(1-a, n, b)としましょう。ここで、F-1bin(1-a, n, b)は、試行n回、成功確率bの二項分布の第(1 - a)分位点です。nが2未満の場合、分布によらない両側許容区間は計算できません。nが2以上の場合、l = floor(n/2)、u = floor(n + 1 - n/2)です。
実際の信頼水準は、Fbin(u-l-1, n, b)で計算されます。ここで、Fbin(x, n, b)は、試行n回、成功確率bの二項分布において、確率変数がx以下になる確率です。
なお、分布によらない両側許容区間を計算するには、標本サイズがnが、次式を満たすようなn以上であることが前提となります。
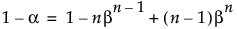
分布によらない許容区間については、Meeker et al.（2017, sec. 5.3）を参照してください。