公開日: 09/19/2023
分散成分の統計的詳細
「変動性図」プラットフォームで選択する正確なモデルの種類は、データの収集方法に依存します。たとえば、複数人の異なるオペレータが同じ部品の組を測定している場合、交差計画になります。複数人の異なるオペレータがそれぞれで異なる部品の組を測定している場合、枝分かれ設計になります。具体例として、BがAから枝分かれしているとして、次のように、na×nb×nw個の測定値があるとします。
• 変量効果Aの水準がna個
• Aの各水準にnb個ずつある変量効果Bの水準がna×nb個
• A内のBの各水準にnw個ずつある変量効果がna×nb×nw個
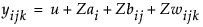
Zは、各階層における変量効果を表します。どのZも、その他の変量効果とは相関がない、平均がゼロの変量効果と仮定されています。この仮定のもとでは、応答Yの分散は、各Z成分の分散の和として求められます。
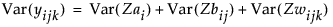
Table 6.3は、使用できるモデルと、各モデル内の効果をまとめたものです。
|
モデル |
因子 |
モデル内の効果 |
|---|---|---|
|
主効果 |
1 2 無制限 |
A A, B 因子数に合わせて以下同様 |
|
交差 |
1 2 3 4 無制限 |
A A, B, A*B A, B, A*B, C, A*C, B*C, A*B*C A, B, A*B, C, A*C, B*C, A*B*C, D, A*D, B*D, A*B*D, C*D, A*C*D, B*C*D, A*B*C*D、 因子数に合わせて以下同様 |
|
枝分かれ |
1 2 3 4 無制限 |
A A, B(A) A, B(A), C(A,B) A, B(A), C(A,B), D(A,B,C) 因子数に合わせて以下同様 |
|
交差後、枝分かれ |
3 |
A, B, A*B, C(A,B) |
|
枝分れ後、交差 |
3 |
A, B(A), C, A*C, C*B(A) |
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).