函数模型拟合

“函数数据分析器”平台中的所有模型拟合依赖于基函数扩展。基函数是一个独立函数集。任意函数 f(t) 可用 K 个基函数的线性组合（表示为 φk）来近似。通常，一个函数按以下方式近似：

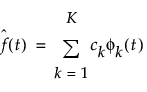
其中 ck 参数是基系数。平滑程度由基函数的数目 K 决定。有关基函数扩展的详细信息，请参见 Ramsay and Silverman (2005)。

傅里叶基函数模型

设有定义傅里叶基函数的 k = 1,..., K 个函数，使 φ0 = 1, φ2k-1 = sin(rωt) 且 φ2k = cos(rωt)。则近似函数表示为：

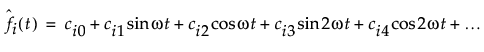
它使用周期 A（定义为 A = 2π/ω）近似一个周期函数。这些系数是固定基函数系数和按函数划分的随机系数的组合。按以下方式定义每个 c：

其中，βk 是基函数 k 的固定系数，αik 是特定函数过程 i 的基函数 k 的随机系数。对于傅里叶基函数模型，βk 和 αik 参数的估计值分别列在“基函数系数”表和“按函数划分的随机系数”表中。

傅里叶基函数模型具有一个截距项和相等数目的正弦和余弦项（称之为傅里叶变换对）。因此，K 始终为奇数。例如，若 K = 7，则有一个截距项和三对傅里叶变换。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).