V 形模板 CUSUM 控制图的统计详细信息
这些公式中使用了以下符号：
• μ 表示总体均值，亦称过程均值或过程水平。
• μ0 表示总体的目标均值（或目标）。有时用符号 
来表示 μ0。请参见 American Society for Quality Statistics Division (2004)。您可以将 μ0 用作启动窗口“CUSUM 图的已知统计量”区域中的“目标”。
• σ 表示总体标准差。
表示 σ 的估计值。
• σ0 表示已知的标准差。您可以将 σo 用作启动窗口“CUSUM 图的已知统计量”区域中的 Sigma。
• n 表示 CUSUM 图的名义样本大小。
• δ 表示要检测的 μ 中的偏移，表示为标准差的倍数。您可以将 δ 用作启动窗口“CUSUM 图的已知统计量”区域中的 Delta。
• Δ 表示要检测的 μ 中的偏移，用数据单位表示。若样本大小 n 在各子组之间保持不变，则适用以下计算：
您可以将 Δ 用作启动窗口“CUSUM 图的已知统计量”区域中的“偏移”。
注意：有些作者使用符号 D 而不是 Δ。
单侧 CUSUM 图
正偏移
若要检测的偏移 δ 为正，第 t 个子组的累积和计算如下：
St = max(0, St – 1+ (zt – k))
t = 1, 2,..., n，其中 S0 = 0，zt 针对双侧图定义，参数 k（称为参考值）为正数。若未在启动窗口中指定参数 k，则将 k 设置为 δ/2。将 CUSUM St 称为上累积和。St 可计算如下：
序列 St 对子组均值中距离 μ0 超过 k 个标准误差的偏差进行累积。若 St 超过正值 h（称为决策区间），则指示偏移或失控状况。
负偏移
若要检测的偏移为负，第 t 个子组的累积和计算如下：
St = max(0, St – 1 – (zt + k))
t = 1, 2,..., n，其中 S0 = 0，zt 针对双侧图定义，参数 k（称为参考值）为正数。若未在启动窗口中指定参数 k，则将 k 设置为 δ/2。CUSUM St 称为下累积和。St 可计算如下：
序列 St 对子组均值中距离 μ0 为 k 个标准误差以内的偏差绝对值进行累积。若 St 超过正值 h（称为决策区间），则指示偏移或失控状况。
请注意，不论 δ 正负如何，St 始终为正，h 始终为正。对于设计用于检测负偏移的图，有些作者定义了 St 的相反版本，即：在 St 小于负限值时指示偏移。
Lucas and Crosier (1982) 描述了 CUSUM 图的快速初始响应 (FIR) 功能的属性，其中的初始 CUSUM S0 设置为“起始值”。他们给出的平均运行链长计算表明 FIR 功能在过程受控时影响极小，所以这导致对初始失控状况的响应速度比标准 CUSUM 图更快。您可以在启动窗口“CUSUM 图的已知统计量”区域中提供“初始值”。
常数样本大小
若子组样本大小为常数 (= n)，最好按照与数据相同的单位来调整和计算累积和。累积和计算如下：
其中，δ > 0
其中 δ < 0。在任何一种情况下，参数 k 按 
重新调整尺度。若未在启动窗口中指定参数 k，则将 k 设置为 δ/2。若 St 超过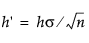 
则指示偏移。某些作者用符号 H 来代替 h'。
双侧 CUSUM 图
若 CUSUM 图为双侧，为第 t 个子组标绘的累积和 St 如下所示：
St = St - 1 +zt
t = 1, 2,..., n。此处的 S0=0，项 zt 计算如下：
其中，
是第 t 个子组的平均值，nt 是第 t 个子组的样本大小。若子组样本由单个测量值 xt 构成，项 zt 简化为以下计算：
zt = (xt – μ0)/σ
第一个方程可重写为以下形式：
其中，序列 St 对距离目标均值 μ0 的子组平均值标准差进行累积。
在许多应用中，子组样本大小 ni 为常数 (ni = n)，St 的方程可简化如下：
在某些应用中，最好按如下方式计算 St：
该式按照与数据相同的单位来调整尺度。在这种情况下，过程将 V 形模板参数 h 和 k 的尺度分别重新调整为 
和 
。某些作者用符号 F 代替 k'，用 H 代替 h'。
若过程处于受控状态且均值 μ 达到目标 μ0 或接近该目标，则采用随机漫步模型。因此，点可能离开零，但是不会呈现大的趋势，因为距离 μ0 的正偏移量和负偏移量趋近于彼此抵消。若 μ 具有正向偏移量，则点呈现向上趋势；若 μ 具有负向偏移量，则点呈现向下趋势。