差分和分解
“时间序列”红色小三角菜单包含以下选项以准备用于建模的数据。
差分
显示“差分说明”窗口(图 18.5)。使用该窗口可以指定要应用于时间序列的差分运算。在时间序列中对值求差分可以将不平稳序列转换为平稳序列。按以下等式给出差分序列:
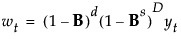
其中 t 是时间索引,B 是由 Byt = yt-1 定义的后移算子。
注意:很多时间序列不具有固定均值,如具有趋势或季节性的时间序列。这样的不平稳序列不适合用假定平稳时间序列的时间序列模型(如 ARMA 模型)来描绘。去除趋势和/或季节性将创建一个平稳的差分序列,使您可以使用假设序列是平稳的模型描绘序列。
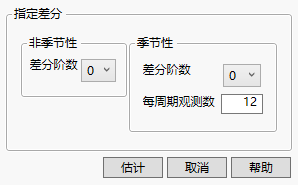
图 18.5 “指定差分”窗口
使用“指定差分”窗口可以指定“非季节性差分阶数”d、“季节性差分阶数”D 和“每周期观测数”s。差分阶数为 0 则相当于没有进行相应的差分运算。每次指定差分运算并点击估计时,将在报表窗口中显示新差分报表。请参见“时间序列”平台的更多示例。
分解
(在启动窗口中选定“针对保留进行预测”或“使用 Box-Cox 变换”时不可用。)显示分解方法的子菜单。时间序列数据的分解用于隔离和去除时间序列中的线性趋势和季节性周期。这有助于更好地估计模型。提供三个“分解”选项。
去除线性趋势
使用线性回归模型估计时间序列的线性趋势并去除数据中的线性趋势。将去除趋势的序列的“时间序列”报表连同线性趋势信息添加到报表窗口。请参见“时间序列”报表和线性趋势报表。
去除周期
使用单个余弦波估计时间序列的周期性成分,然后将它从数据中去除。选择“删除周期”选项时,显示“定义周期”对话框。使用该对话框窗口,您可以指定每个周期的单位数并指示是否应从数据中减去一个常数。将去除周期的序列的“时间序列”报表连同周期信息添加到报表窗口。请参见“时间序列”报表和周期报表。
X11
使用美国人口普查局开发的 X-11 方法(Shiskin 等人 1967)去除趋势和季节效应。有关 X-11 方法的详细信息,请参见X-11 分解的统计详细信息。选中时,显示“选择分解类型”对话框。使用该对话框窗口可以指定乘法或加法的 X-11 调整。点击确定后,将一个 X11 报表添加到报表窗口。请参见X11 报表。
X11 选项仅适用于每月或每季度数据。X,时间 ID 列必须为按月度或季度等间距分隔的数值列,不能有任何时间间隔或缺失值。若用来进行 X11 分析的时间列不满足这些要求,JMP 会返回错误。有关 X11 分析的适当时间列的示例,请参见创建合适的“时间 ID”列。
注意:选择去除线性趋势或去除周期选项时,JMP 将一列添加到数据表,其中包含去除趋势或去除周期的数据。若选择该选项时该列在数据表中已存在,JMP 将覆盖现有列。
提示:通常您按以下顺序开始分解:删除任何线性趋势,然后删除长周期(如 12 个月的周期),接着删除短周期(如 6 个月的周期)。
显示滞后图
显示或隐藏一个图,它在 Y 轴上具有时间 t 处的观测,在 X 轴上具有时间 t +/- p 处的观测。+/- p 即为滞后。该图可帮助确定时间 t 处的观测与时间 t +/- p 处的观测的关系。若该图不存在可识别的结构,则这些观测不相关。但是,若该图存在明显的结构,则指示跨越时间的观测之间存在一定关系。构建时间序列模型时,标识该结构很有帮助。
显示 Box-Cox 变换图
(若在启动窗口中指定了“使用 Box-Cox 变换”则不可用。)显示或隐藏 Box-Cox 变换图。Box-Cox 变换是基于 Lambda 参数 (l) 的幂变换并使用以下公式:
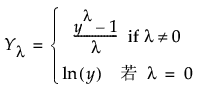
Box-Cox 变换图显示变换后的时间序列图和用于设置 Lambda 参数 (l) 的选项。Lambda 框显示参数的当前值。您还可以使用 Lambda 滑块更改参数的值,更改后会自动更新该图。“下限”框和“上限”框设置滑块的范围。
提示:使用 Box-Cox 变换图可查看不同的 Lambda 值的变换时间序列。一旦决定使用某个值,重新启动分析并选择使用 Box-Cox 变换,然后在“Box-Cox 的 Lambda”旁边输入所需的 Lambda。这会针对变换的序列运行“时间序列”平台。
交叉相关性
(仅在“转换函数分析”红色小三角菜单中可用。)在报表上显示或隐藏交叉相关性图。该图的长度是自相关图长度的两倍,或 2 × ACF 长度 + 1。该图同时以数值和图形的形式展示了输出序列相对于所有输入序列的相关性。蓝线指示两个标准误差。
注意:对于交叉相关图,原假设下标准误差计算为 1/平方根(n - k),其中,n 是非缺失数据值的数量,k 是自相关滞后期数。
预白化
(仅在“输入序列”红色小三角菜单中可用。)显示“指定预白化”窗口,您可以在其中设置预白化阶数。预白化是用于帮助标识转换函数模型的方法。这种方法涉及拟合输入序列的 ARIMA 模型,以便残差等同于白噪声。同一模型随后用于估计输出序列。您可以使用过滤的输入和过滤的输出序列之间的交叉相关性来确定适用于转换函数模型的滞后。有关预白化的信息,请参见 Box 等人 (1994)。