拟合简单生存分布的示例
本节包含在“非线性”平台中拟合简单生存分布的示例。
指数、Weibull 和极值损失函数
您可以使用“非线性”平台拟合失效时间数据的指数、Weibull 和极值损失函数。本例中的数据来自对 70 台柴油机风扇的研究,这些风扇累计运行超过 30 万小时。风扇在不同的时间投入使用。响应是风扇的失效时间或删失处的运行时间。
1. 选择帮助 > 样本数据文件夹,然后打开 Reliability/Fan.jmp。
提示:要查看损失函数的公式,请在 Fan.jmp 数据表中,右击指数、Weibull 和极值列并选择公式。
2. 选择分析 > 专业建模 > 非线性。
3. 选择指数并点击损失。
4. 点击确定。
5. 确保选中损失为负的对数似然复选框。
6. 点击执行。
7. 点击置信限。
8. 重复这些步骤,但选择 Weibull 和极值而不是指数。
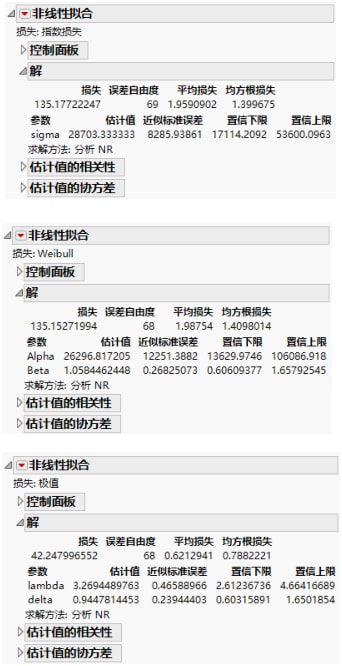
图 15.28 非线性拟合结果
对数正态损失函数
对数正态分布在数据范围为 e 的若干次幂时很有用。对数正态损失函数可能对其参数的起始值非常敏感。因为对数正态分布与正态分布相似,您可以创建是时间的自然对数的新变量并使用分布来查找该列的均值和标准差。之后,将这些值用作“非线性”平台的起始值。在本例中,时间的自然对数均值为 4.72,标准差为 0.35。
1. 选择帮助 > 样本数据文件夹,然后打开 Reliability/Locomotive.jmp。
提示:要查看损失函数的公式,请在 Locomotive.jmp 数据表中右击对数正态列并选择公式。
2. 选择分析 > 专业建模 > 非线性。
3. 选择对数正态并点击损失。
4. 点击确定。
5. 在“Mu”旁边的框中键入 4.72。
6. 在“Sigma”旁边的框中键入 0.35。
7. 点击执行。
8. 点击置信限。
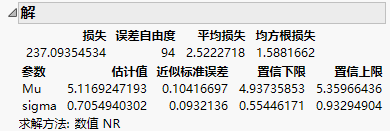
图 15.29 “解”报表
对数正态参数的最大似然估计值对于 Mu 为 5.11692,对于 Sigma 为 0.7055。对数正态分布的中位数的相应估计值为 5.11692 的反对数 (e5.11692),该值约为 167。该值表示机车发动机的典型寿命。