加速寿命试验的最优性准则

考虑加速寿命试验 (ALT) 最多在两个加速因子 x1 和 x2（分别具有 J1 和 J2 个水平）之间进行。试验计划的目标是确定分配给每个因子水平组合的样本数。

最优性准则的计算依赖于来自单个水平特定信息矩阵的总体 Fisher 信息矩阵

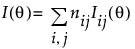
以及在适当的情况下包含先验不确定性 S。

D 最优性

D 最优设计 Dd 是使下列表达式在 njj 的所有可能值上最小化的设计

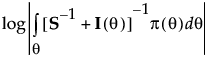
其中 |·| 是行列式运算，p(q) 是参数的先验分布。该分布通常为多元正态分布。行列式的对数用于数值稳定性。

分位数最优性

分位数最优设计 Dq 是使以下表达式最小化的设计：

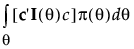
其中，向量 c 取决于使用条件。

对于单一使用条件

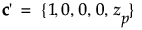
其中，zp 是失效分布的第 p 分位数。

对于使用条件范围，令

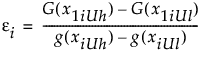
其中，G(·) 是 g(·) 的反导数，xiUh 是为第 i 个因子考虑的最高使用水平，xiUl 是为同一因子考虑的最低使用水平。那么

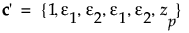
其中，zp 是失效分布的第 p 分位数。

失效概率最优性

失效概率最优设计 Df 是使以下表达式最小化的设计：

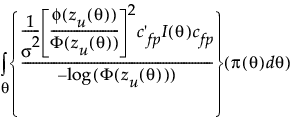
其中，zU(θ) 是如分位数最优性中定义的使用条件下的标准化对数时间。cfp 类似于分位数最优性中定义的 c，只不过最后一项是 zU(θ)。分子中的量基于 logΦ(zU(θ)) 的渐近方差，其中对数变换用于数值稳定性。随后按照原始 logΦ(zU(θ)) 对渐进方差标准化以便保持一致，且越小越好。对于一定范围的使用条件，积分取在对数 logΦ(·) 内而不是对渐近方差取积分，以便于计算。作为一个最优性量度，它在性质上仍然是合适的，因为方差之和以总和方差为界限，并且对数函数和 cdf 都是单调函数。因此，上述表达式的最小化通过从上述限定失效概率来最小化失效概率的真实渐近方差。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).