“拟合曲线”平台概述

某些模型在参数上是线性的（例如，二次式或其他多项式）；而某些模型的参数可变换为线性（例如，在您使用 x 的对数变换时）。“拟合模型”或“以 X 拟合 Y”平台在这些情形下更适用。《拟合线性模型》中的“使用“拟合模型”的回归分析示例”中的示例显示了吸氧量与跑步时间之间存在显著的线性关系。有关“拟合模型”的详细信息，请参见《拟合线性模型》中的“模型规格”。有关“以 X 拟合 Y”的详细信息，请参见《基本分析》中的“Introduction to Fit Y by X”。

“拟合曲线”平台支持您拟合参数上非线性的模型。本章中的第一个示例将展示一个非线性关系的分析：药物毒性是浓度的函数， 但浓度对于毒性的影响随着剂量由低到高发生变化，所以这种关系是非线性的。

下面列出了线性和非线性函数的方程的示例。

线性函数：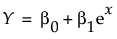

非线性函数：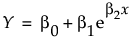

“拟合曲线”平台提供预定义的模型，如多项式、Logistic、Probit、Gompertz、指数、峰值、药代动力学、比率和溶解模型。指定分组变量允许您为分组变量的每个水平分别估计模型参数， 因此您可以比较分组变量各水平下的拟合模型和估计参数。还有一组选项可用于比较溶解曲线，包括参数和非参数方法选项。

“拟合曲线”还支持您构建模型以创建预测公式。之后您可以在“非线性”中设置参数上限和下限。请参见“设置参数限值的示例”。在 JMP Pro 中，还可以指定一组补充变量，并在“拟合曲线”平台中拟合广义回归模型，以确定这些变量如何影响响应。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).