连续拟合分布的统计详细信息
本节包含“分布”平台的“连续拟合”菜单中的选项的统计详细信息。除非另有规定，参数估计值的置信区间使用基于似然的计算。若 Y 列具有“检测限”列属性，则“连续拟合”选项拟合删失分布，并且只有部分分布可用。有关拟合删失数据的分布的详细信息，请参见 Meeker and Escobar (1998)。
拟合正态
“拟合正态”选项估计正态分布的两个参数：
• m（均值）定义分布在 x 轴上所处的位置
• s（标准差）定义分布的离散或散布程度
当 m = 0 且 s = 1 时出现标准正态分布。
pdf: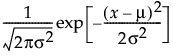 
; 
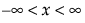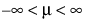; 0 < s
E(x) = m
Var(x) = s2
注意：均值估计值的置信区间基于 t 分布。尺度参数的置信区间基于 c2 分布。
拟合 Cauchy
“拟合 Cauchy”选项使用位置 m 和尺度 s 拟合 Cauchy 分布。
pdf: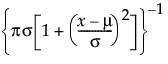 
; 
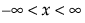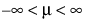; 0 < s
E(x) = 未定义
Var(x) =未定义
拟合 Student t
“拟合 Student t”选项拟合位置为 m、尺度为 s 且自由度为 n 的 Student t 分布。
pdf: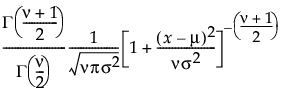 
; 
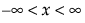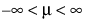; 0 < s; 1 ≤ n
拟合 SHASH
“拟合 SHASH”选项拟合 sinh-arcsinh (SHASH) 分布。SHASH 分布基于变换了的正态分布，它将正态分布作为特例包括在内。该分布可以对称也可以非对称。形状由两个形状参数 g 和 d 决定。有关 SHASH 分布的详细信息，请参见 Jones and Pewsey (2009)。
pdf: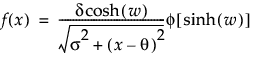 
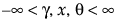; 0 < d, s
其中
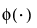是标准正态 pdf
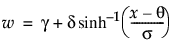
• 当 g = 0 且 d = 1 时，SHASH 分布等价于位置为 q 且尺度为 s 的正态分布。
• 变换 sinh(w) 服从 m = 0 且 s = 1 的正态分布。
拟合指数
指数分布尤其适用于描述随时间随机出现的事件，如生存数据。指数分布可能还适用于对不重叠事件各次出现之间经过的时间进行建模。不重叠事件的示例包括以下几项：用户计算机查询与服务器响应之间的时间、客户先后到达服务台相隔的时间，或是传入交换机的各次呼叫之间的时间。
“指数”分布是双参数 Weibull 在 b = 1 且 a = s 时的特例，也是 Gamma 分布在 a = 1 时的特例。
pdf: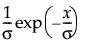 
0 < s; 0 ≤ x
E(x) = s
Var(x) = s2
Devore (1995) 提出指数分布是无记忆的。无记忆意味着若您在 t 小时后检查某个部件，而该部件仍然在运转，此时附加寿命时间的分布（该部件一直存活到 t 时刻情形下的附加寿命的条件概率）与原始分布相同。
拟合 Gamma
“拟合 Gamma”选项估计 gamma 分布参数，a > 0 和 s > 0。参数 a（在拟合 gamma 报表中称为 alpha）描述形状或曲率。参数 s（称为 Sigma）是分布的尺度参数。数据必须大于零。
pdf: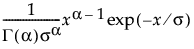 
0 < x; 0 < a,s
E(x) = as
Var(x) = as2
• 标准 gamma 分布的 s = 1。Sigma 称为尺度参数，因为 1 之外的值将沿着水平轴延展或收缩分布。
• 当 s = 2 且 a = n/2 时呈卡方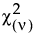 
分布。
• 当 a = 1 时呈指数分布。
当 a ≤ 1 时，标准 gamma 密度函数严格递减。当 a > 1，密度函数从 0 开始，增加到最大值，然后递减。
拟合对数正态
“对数正态”选项估计双参数对数正态分布的参数 m（尺度）和 s（形状）。当且仅当 X = ln(Y) 服从正态分布时，变量 Y 服从对数正态分布。数据必须大于零。
pdf: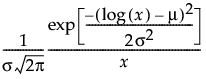 
; 
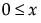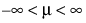; 0 < s
E(x) =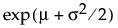 
Var(x) =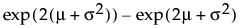 
拟合 Weibull
Weibull 分布根据 a（尺度）和 b（形状）的值呈不同形状。它通常为估计寿命（特别是机械设备和生物方面）提供合适的模型。
Weibull 分布的 pdf 定义如下：
pdf: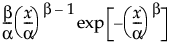 
a,b > 0; 0 < x
E(x) =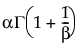 
Var(x) =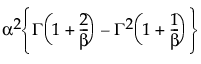 
其中，G(·) 是 Gamma 函数。
拟合两正态混合和拟合三正态混合
“拟合两正态混合”和“拟合三正态混合”选项可拟合混合的两个或三个正态分布。这些灵活的分布能够拟合双模态或多模态数据。将为每个分组估计单独的均值、标准差和占整体的比例。在下面的方程中，k 等于混合中的正态分布数目。
pdf: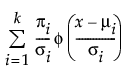 
E(x) =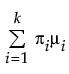
Var(x) =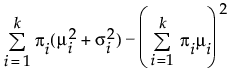
其中，mi、si 和 pi 分别是第 i 个分组的均值、标准差和比例；f(·) 是标准正态 pdf。
注意：正态混合分布参数估计值的置信区间使用基于 Wald 的计算。
拟合 Johnson
“拟合 Johnson”选项用于选择并拟合 Johnson 分布体系中的最佳拟合分布，Johnson 分布体系包含三个分布，这三个分布全部基于变换正态分布。这三种分布如下：
• Johnson Su，无界。
• Johnson Sb，双侧均有界限。这些界限由可以估计的参数定义。
• Johnson Sl，单侧有界限。该界限由可以估计的参数定义。Johnson Sl 系列包含一系列对数正态分布。
仅报告选定分布的拟合。有关 Johnson 分布的选择过程和参数估计的信息，可以在 Slifker and Shapiro (1980) 中找到。参数估计不使用最大似然。
Johnson 分布十分灵活，所以很受欢迎。特别是，Johnson 分布体系以其数据拟合能力闻名，因为它支持偏度和峰度的每种可能组合。不过，SHASH 分布也是非常灵活的，相对于 Johnson 分布，优先推荐使用 SHASH 分布。
若 Z 是标准正态变量，则该体系定义如下：
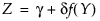
其中，对于 Johnson Su：
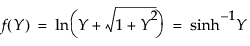
其中，对于 Johnson Sb：
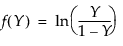
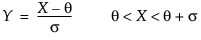
对于 Johnson Sl，其中 s = ±1。
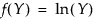
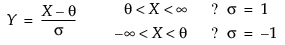
Johnson Su
pdf: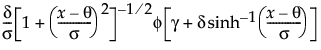 
-∞ < x, q, g < ∞; 0 < q,d
Johnson Sb
pdf: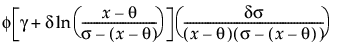 
q < x < q+s; 0 < s
Johnson Sl
pdf: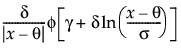 
q < x 若 s = 1; q > x 若 s = -1
其中 f(·) 是标准正态 pdf。
注意：Johnson 分布参数估计值的置信区间使用基于 Wald 的计算。
拟合 Beta
beta 分布适用于对限制在 0,1 区间内的随机变量的行为建模。例如，比例总是介于 0 和 1 之间。“拟合 Beta”选项估计两个形状参数：a > 0 和 b > 0。beta 分布的值仅位于区间 0,1 中。
pdf: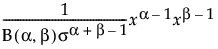 
0 < x < 1; 0 < s,a,b
E(x) =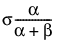 
Var(x) =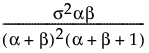 
其中 B(·) 是 Beta 函数。
全部拟合
在“比较分布”报表中，“分布”列表按 AICc 升序排序。使用复选框可显示或隐藏拟合报表以及叠加选定分布的曲线。
AICc 和 BIC 的公式定义如下：
AICc =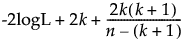
BIC =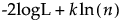 
其中：
– logL 是对数似然。
– n 是样本大小。
– k 是参数个数。
“AICc 权重”列显示加总为 1 的标准化 AICc 值。AICc 权重可解释为在其中的一个拟合分布成立的前提下，特定分布为真实分布的概率。因此，AICc 权重最接近 1 的分布是更好的拟合。仅使用非缺失 AICc 值计算 AICc 权重：
AICc 权重 = exp[-0.5(AICc-min(AICc))] / sum(exp[-0.5(AICc-min(AICc))])
其中，min(AICc) 是拟合分布中的最小 AICc 值。
有关“比较分布”报表中的测度的详细信息，请参见《拟合线性模型》中的“似然、AICc 和 BIC”。