贡献的统计详细信息

本节包含“模型驱动的多元控制图”平台中的贡献统计量的计算。

T2

具有 p 个变量和 k 个成分的 PCA 或 PLS 模型的 T2 贡献计算如下：

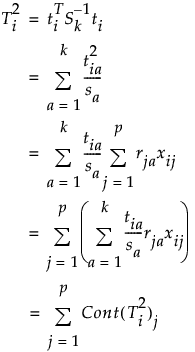
其中：

ti = 第 i 个观测的 k 得分的向量

Sk = 历史观测的 k 得分的对角线样本协方差矩阵。对于 PCA 模型，Sk 是对角线特征值矩阵。

sa = Sk 的第 a 个对角线元素

rja = 对于 PCA 模型是第 a 个特征向量的第 j 个元素，对于 PLS 模型则是 Rk 载荷矩阵的第 a 列。Rk 是用于将得分矩阵 Tk 关联到 X 矩阵的矩阵，使得 Tk=XRk。

xij = 第 i 个观测的第 j 个变量的值。

注意：最后一个总和中的 p 项数是变量贡献。

每个变量的贡献是其对每个得分的贡献之和，按标准化得分值来加权。若标准化得分值较大，且变量贡献较大，则认为变量对 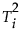的贡献较大。

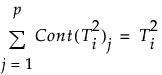
变量 j 的贡献比例定义为：

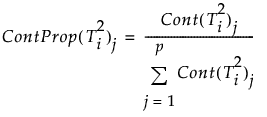
注意：计算 T2 贡献比例时，JMP 会将负贡献归零。在 PCA 和 PLS 模型中，由于变量在 X 投影时的交互作用，可能会产生负贡献。负贡献清零，以确认表示占总的正贡献较大比例的变量贡献。

有关 PCA 贡献和负贡献的详细信息，请参见 Kourti and MacGregor (1996)。有关 PLS 贡献的详细信息，请参见 Li et al.(2009)。

DModX

对于 PCA 和 PLS 模型，变量 j 对 DModXi 的贡献定义如下：

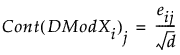
请注意，由于

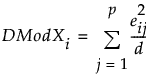
变量 j 的贡献比例定义为：

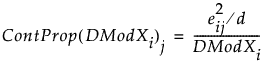
SPE

对于 PCA 和 PLS 模型，变量 j 对 SPEi 的贡献定义如下：

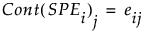
请注意，由于

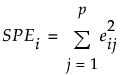
变量 j 的贡献比例定义为：

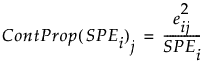
得分贡献

得分贡献计算与 T2 贡献相同，但仅针对得分图中选定的维进行计算。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).