监控统计量的统计详细信息

本节包含“模型驱动的多元控制图”平台中的监控统计量的计算。

T2

每个 i 观测的 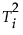值都绘制在 T2 控制图上。对于历史和当前数据，具有 k 个成分的 PCA 或 PLS 模型的 T2 值定义如下：

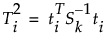
其中：

ti = 第 i 个观测的 k 得分的向量

Sk = 历史观测的 k 得分的对角线样本协方差矩阵

对于 PCA 模型，Sk 是对角线特征值矩阵。

当数据在数据预处理步骤中已中心化时，k 个历史得分向量的均值为 0。该步骤发生在基于相关性或协方差的 PCA 以及进行中心化的 PLS 中。对于 X 未中心化的预处理选项，则假设数据已经由用户中心化，所以每个 k 得分向量的均值为 0。有关 Hotelling’s T2 的详细信息，请参见 Montgomery (2013)。

SPE

对于 PCA 和 PLS 模型，预处理的 X 矩阵可分解为：

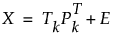
其中，Tk = (t1,...,tk) 是 k 维得分矩阵，Pk = (p1,...,pk) 对于 PCA 模型是具有前 k 个特征向量的矩阵，而对于 PLS 模型是载荷矩阵。该 PCA 或 PLS 模型的平方预测误差用于 SPE 控制图。

每个 i 观测的 SPEi 值都绘制在 SPE 控制图上。平方预测误差定义为：

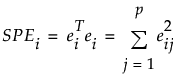
其中

ei = 观测 i 的残差向量

p = 变量数

DModX

每个 i 观测的 DModXi 值都绘制在 DModX 控制图上。与模型的标准化距离 (DModX) 定义为：

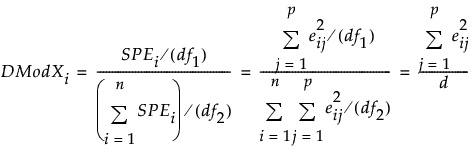
其中

eij = 观测 i 和变量 j 的残差

df1 = p−k

df2 = (n−k−1)(p−k)（若数据已中心化）；或为 (n−k)(p−k)（若数据未中心化）

n = 历史数据观测数

k = PCA/PLS 成分数

p = 变量数

注意：DModXi 等于以 1/d 为尺度的 SPEi。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).