宽方法的统计详细信息
本节包含在“主成分”启动窗口中将“宽数据”指定为“方法系列”时使用的估计方法的统计详细信息。这些方法基于奇异值分解 (SVD)。这避免了计算协方差矩阵,从而使这些方法成为计算高效的算法。
完全 SVD
“完全 SVD”方法使用基于矩阵的完全奇异值分解的算法。考虑以下符号:
• n = 行数
• p = 变量数
• X = 数据值的 n x p 矩阵
非零特征值数以及得到的主成分数均等于 X 的相关性矩阵的秩。非零特征值数不得超过 n 和 p 中较小的那个值。
在实施“完全 SVD”方法之前,数据已标准化。要将某个值标准化,需减去其均值,再除以其标准差。用 Xs 来表示标准化数据值的 n x p 矩阵。之后,标准化数据的协方差矩阵成为 X 的相关性矩阵,该矩阵定义如下:
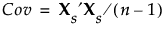
使用奇异值分解,Xs 可表示为 UDiag(Λ)V′。这种表示法用于获取 Xs′Xs 的特征向量和特征值。主成分或得分通过 XsV 计算得出。更多背景信息,请参见““宽线性”方法和奇异值分解”。
 截断 SVD
截断 SVD
“截断 SVD”方法使用基于奇异值分解但不执行完全分解的算法。而该算法在奇异值分解时仅计算第一个指定数量的奇异值和奇异向量。因此,只返回第一个指定数量的特征值和主成分。有关算法的详细信息,请参见 Baglama and Reichel (2005)。
随机化 SVD
“随机化 SVD”方法使用基于奇异值分解但不执行完全分解的算法。该算法是一个涉及低秩矩阵近似的两步过程。通常,低秩矩阵近似的目标是要近似计算一个 m × k 矩阵 A,方法是查找 m × k 矩阵 B 和 k × p 矩阵 C,以使 k 远远小于 p 且 A ≈ BC。
考虑完全 SVD中所述的相同符号,其中的目标是要分解 Xs。
在“随机化 SVD”算法的第一步中,获得矩阵 Q,使得以下条件成立:
• Q 具有 l 个正交列,其中 k ≤ l ≤ p
• Xs ≈ QQ′Xs
关于高效计算 Q 使其具有尽量少的列的详细信息,请参见 Halko, Martinsson, and Tropp (2011)。
算法的第二步使用 Q 来计算 Xs 的奇异值分解。令 B = Q′Xs。然后,以下条件成立:
B = Q′Xs ⇒ QB = QQ′Xs ⇒ QB = Xs
然后,计算 B 的 SVD(远远小于 Xs):
B ≈ U*Diag(Λ)V′
QB ≈ (QU*)Diag(Λ)V′
A ≈ UDiag(Λ)V′,其中 U = QU*
有关完整的“随机化 SVD”算法的详细信息,请参见 Halko, Martinsson, and Tropp (2011)。