“对数线性方差拟合”报表

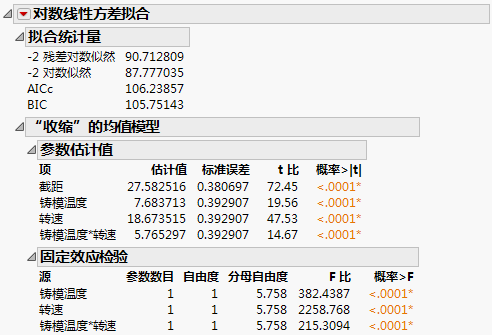
“对数线性方差拟合”报表包含有关总体模型、均值模型和方差模型的信息。报表中还包含对数线性模型的预测值-实际值图。均值模型和方差模型报表的“参数估计值”和“固定效应检验”部分类似于在“标准最小二乘法”特质中提供的输出，尽管它们来自限制最大似然 (REML)。

图 11.4 均值模型输出 

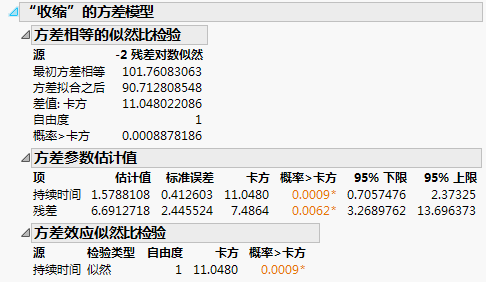
图 11.5 方差模型输出 

报表的第二部分显示方差模型的拟合。“方差参数估计值”报表显示估计值和相关统计量。提供两个隐藏的列：

• 隐藏的列 exp(Estimate) 是估计值的指数。因此，若将这些因子编码为具有 +1 和 -1 值，则因子的 +1 水平将具有方差与 exp(Estimate) 值相乘所得的值。同样，-1 水平将具有方差与该列倒数相乘所得的值。要查看隐藏的列，可右击报表并从显示的列菜单中选择列的名称。

• 若回归变量的范围为 -1 到 +1，则标记为 exp(2|Estimate|) 的隐藏列是较大方差与较小方差之比。

该报表还显示每个估计值的标准误差、卡方、p 值和刻画似然置信限。残差参数是方差的总估计值，假设所有其他回归变量都是零。

方差模型拟合是否显著好于原始模型？针对该问题的似然比检验比较了拟合模型和除截距外所有参数均为零的模型（即相等方差的模型）。在本例中，p 值是高度显著的。持续时间的变化导致方差变化。

方差效应似然比检验通过重新拟合依次不含每项的模型来创建似然比检验。这些检验通常比 Wald 检验更可信。