在饱和设计中，试验次数等于模型项的个数。在超饱和设计中，模型项数超过了试验次数 (Lin, 1993)。超饱和设计可使用比因子数一半还少的试验次数来检查几十个因子。于是在因子数众多而试验成本高昂的情况下，超饱和设计便成了颇具吸引力的因子筛选选择。
|
•
|
若实验中的活跃因子个数超过了试验次数的一半，则这些因子可能无法识别。一般规则是：试验次数应至少是活跃因子个数的四倍之多。换言之：若您预计活跃因子可能多达五个，那么应计划执行至少 20 次试验。
|
|
•
|
|
1.
|
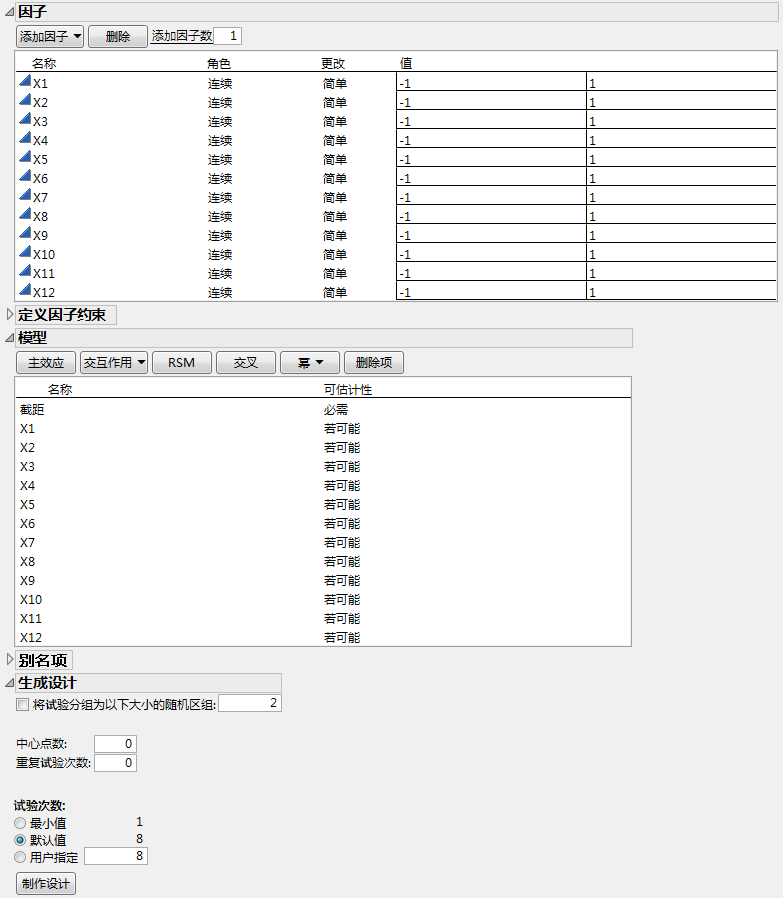
选择实验设计 > 定制设计。
|
|
2.
|
在添加因子数旁边键入 12。
|
|
3.
|
点击添加因子 > 连续。
|
|
4.
|
点击继续。
|
|
6.
|
将效应设置为若可能可确保 JMP 使用 Bayes D 最优性准则获取设计。
图 5.12 因子、模型和试验次数
|
7.
|
|
8.
|
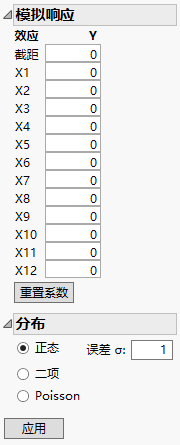
从红色小三角菜单中选择模拟响应。
|
|
9.
|
|
10.
|
|
11.
|
点击制作设计。
|
|
12.
|
点击制表。
|
图 5.13 包含模拟响应的设计表
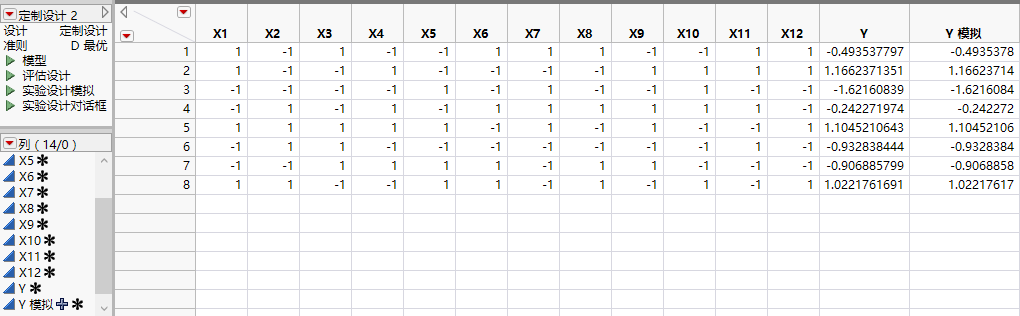
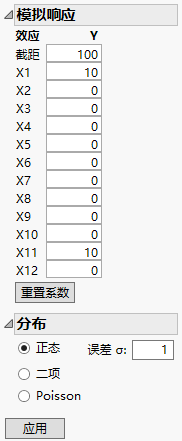
响应列 Y 和 Y 模拟的初始值具有相同的模拟值。这些值是来自 N(0, s) 分布 的随机值。其中，s 是来自功效分析对话框的 RMSE，默认值为 1。Y 模拟值随着使用“模拟响应”窗口中的参数值定义的模型随机生成的值而更新。Y 列专用于运行实验后的真实响应。
图 5.14 “模拟响应”窗口
|
13.
|
图 5.15 模拟响应的参数值
|
14.
|
点击应用。
|
|
1.
|
在设计表的“表”面板中，点击筛选脚本旁边的绿色小三角。
|
图 5.17 超饱和设计的筛选报表
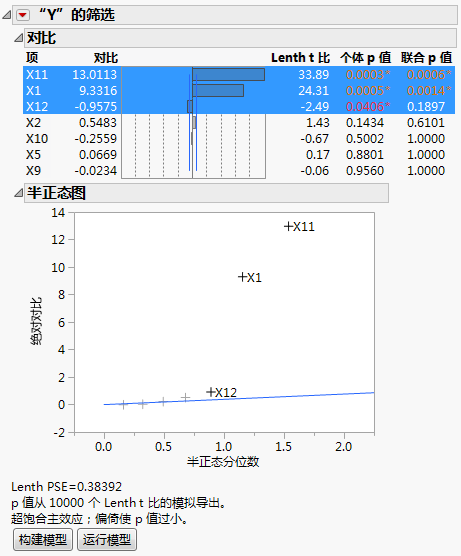
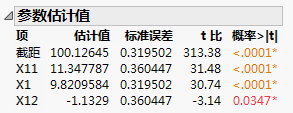
因子 X1 和 X11 具有较大的对比以及 Lenth t 比值。此外，这两个因子的“联合 p 值”较小。在半正态图中，X1 和 X11 均落在距离线条较远的位置。“对比”报表和“半正态图”报表指示 X1 和 X11 是活跃的。尽管 X12 的“个体 p 值”小于 0.05，但其效应比 X1 和 X11 的效应小得多。
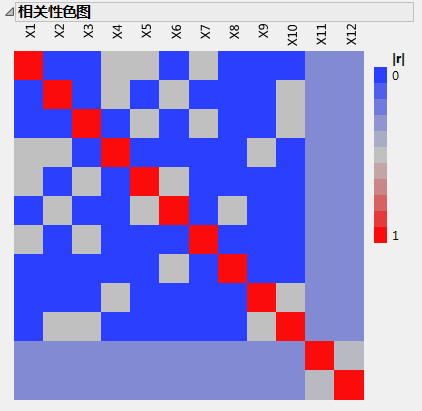
您可能还需要检查显示为活跃的效应是否与其他效应高度相关。若高度相关，则一个效应可能会掩盖另一个效应的真正显著性。图 5.19中的色图显示效应之间的绝对相关性。
|
2.
|
点击构建模型。
|
|
3.
|
图 5.18 模型的参数估计值
|
4.
|
在“定制设计”窗口中，打开设计评估 > 相关性色图分级显示项。
|
图 5.19 “相关性色图”分级显示项
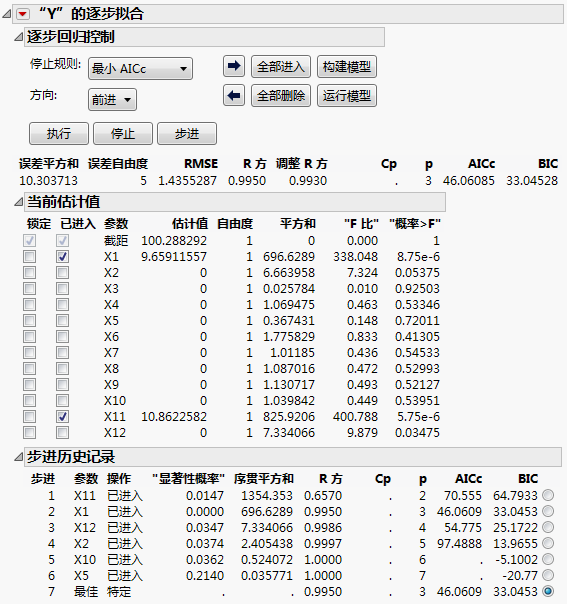
逐步回归是另一种标识活跃因子的方式。图 5.16中的设计表包含三个脚本。“模型”脚本使用“拟合模型”平台中的逐步回归分析数据。
|
1.
|
在设计表的“表”面板中，点击模型脚本旁边的绿色小三角。
|
|
2.
|
|
3.
|
点击运行。
|
|
4.
|
|
5.
|
点击执行。
|
图 5.20 超饱和设计的逐步回归
