该帮助的版本不再更新，请参见https://www.jmp.com/support/help/zh-cn/15.2 获取最新的版本.


拟合线性模型 • 广义回归示例 • 零泛滥 Poisson 回归的示例
上一个
 • 
下一个
零泛滥 Poisson 回归的示例
Fishing.jmp 样本数据表包含虚拟数据，用于研究哪些因素会影响成组游客在公园里钓到的鱼的数目。该数据表包含结伴而来的家庭或团体的 250 个响应。本例将钓鱼数建模为活鱼饵、鱼竿、露营者、人和儿童的函数。数据表的“列注释”中对这些列进行了说明。
该数据表包含名为钓过鱼的隐藏列。在数据收集期间，它从不确定组中的任何人是否实际钓鱼了。但是，将钓过鱼列包括在表中以强调在以下两种情况下钓鱼数可以为零：组中没有一个人在钓鱼或组中钓鱼的人运气都很不好。
因此，零响应可能有两个来源。要解决该问题，您可以拟合零泛滥分布。因为 Poisson 分布适用于来自钓鱼的人的计数数据，您拟合零泛滥 Poisson 分布。
1.
选择帮助 > 样本数据库，然后打开 Fishing.jmp。
2.
选择分析 > 拟合模型。
3.
从“选择列”列表中选择钓鱼数，然后点击 Y。
4.
从活鱼饵一直选到儿童，然后点击宏 > 析因次数。
这会将最高达到 2 次（次数框中的默认值）的所有项都添加到模型中。
5.
从“选择列”列表中选择“验证”，然后点击验证。
6.
从“特质”列表中选择广义回归。
7.
从“分布”列表中选择零泛滥 Poisson。
8.
点击运行。
显示的“广义回归”报表包含“模型启动”控制面板和一个“使用‘验证列’验证的最大似然”报表。请注意，默认估计方法是“自适应 Lasso”。
9.
从“估计方法”列表中，选择弹性网络。
10.
点击执行。
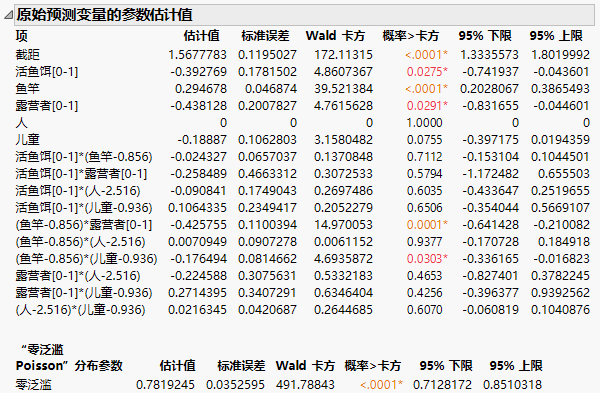
随即显示“使用‘验证列’验证的自适应弹性网络”报表。“解路径”、“原始预测变量的参数估计值”报表和“效应检验”报表都指示很多项为零。零泛滥参数（其估计值显示在两个参数估计值报表的最后一行）高度显著。这指示响应钓鱼数中的一些变异可能是一些组实际不钓鱼造成的。
图 7.6 “原始预测变量的参数估计值”报表
“效应检验”报表指示以下五个项在 0.05 水平下是显著的：活鱼饵、鱼竿、露营者、鱼竿*露营者和鱼竿*儿童。
11.
点击“使用验证列的自适应弹性网络”旁边的红色小三角，然后选择刻画器 > 刻画器。
12.
点击“预测刻画器”红色小三角菜单并选择最优化和意愿 > 意愿函数。
响应应用了一个函数，它指示最大化钓鱼数是您想要的。（有关意愿函数的详细信息，请参见《刻画器指南》手册中的“刻画器”。）
13.
点击“预测刻画器”红色小三角菜单并选择最优化和意愿 > 最大化意愿。
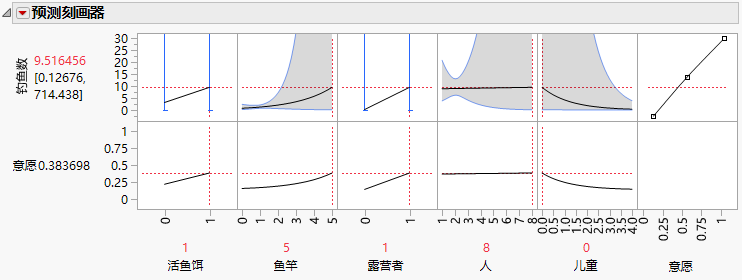
图 7.7 最大化钓鱼数的“预测刻画器”
您可以更改预测变量的设置来查看以下显著效应的影响：活鱼饵、鱼竿、鱼竿*露营者和鱼竿*儿童。例如，活鱼饵与钓到更多的鱼关联；露营者与不露营的人相比带来的鱼竿更多，因此钓的鱼更多。
14.
点击“使用‘验证列’验证的自适应弹性网络”旁边的红色小三角，然后选择保存列 > 保存预测公式和保存列 > 保存方差公式。
以下两列添加到数据表：“钓鱼数”预测公式和“钓鱼数”方差。
15.
右击列标题并选择公式以查看公式。或者，点击“列”面板中列名称右侧的加号。请注意，估计的零泛滥参数 0.7819268 在这两个公式中都出现了。