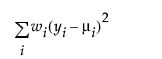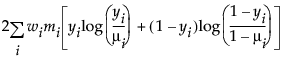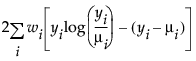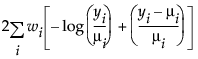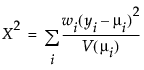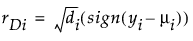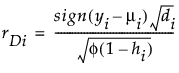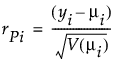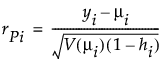广义线性建模的一个重要方面是模型中解释变量的选择。拟合优度统计量的变化通常用于评估解释变量的子集对特定模型的贡献。将偏差定义为可达到的最大对数似然与回归参数的最大似然估计值处的对数似然的差值的两倍。偏差通常用作拟合优度的测度。使用每个观测对应有参数的模型能够实现可达到的最大对数似然。响应分布的偏差公式列出响应变量的每个可用分布的偏差公式。
μi 是相应的预测均值
分布为非正态时,使用正态临界值来替代逆预测的 t 分布临界值。
φ 是离散参数