在一些情形下(如重复测量模型),允许将多元问题变换为一元问题 (Huynh and Feldt 1970)。在以下情形下在多元环境中使用一元检验是有效的:
|
•
|
|
•
|
若 M 生成多个响应且每个变换的系数之和为零。
|
|
•
|
若保持这些条件,则对 E 和 H 检验矩阵的对角线元素求和,以生成 F 检验的分母和分子的一元平方和。请注意,若不保持上述条件,将显示错误消息。在 Golf Balls.jmp 的案例中,单位矩阵指定为 M 矩阵。在列向量中心化和正交化后,单位矩阵不能变换为满秩矩阵。因此忽略一元请求。
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
对于“特质”,请选择多元方差分析。
|
|
7.
|
点击运行。
|
|
8.
|
选中进行一元检验旁边的复选框。
|
|
9.
|
应为“Y 名称”输入“时间”,应选中进行一元检验。
|
10.
|
点击确定。
|
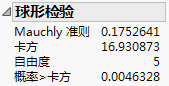
球形检验使用 Mauchly 准则检查对象内效应的未调整的一元 F 检验是否合适,以检验球形假设 (Anderson 1958)。始终使用正交化的 M 矩阵进行球形检验和一元检验。您按以下方式解释球形检验:
|
•
|
若真正的协方差结构为球形,您可以使用未调整的一元 F 检验。
|
一元 F 统计量具有近似 F 分布(即使不含球形),但分子和分母的自由度大约减少了分数 epsilon (ε)。Box (1954)、Greenhouse and Geisser (1959) 以及 Huynh-Feldt (1976) 提供估计 epsilon 自由度调整的方法。Muller and Barton (1989) 基于功效的研究建议采用 Greenhouse-Geisser 版本。