常用的变换是将响应升高到特定次幂。Box and Cox (1964) 对这一系列的幂变换进行了规范化和说明。构造该变换的公式以便按照参数 λ 提供连续定义,这样即可比较误差平方和。具体而言,以下方程提供了一系列的变换:
“Box-Cox Y 变换”选项对从 λ = –2 到 2(增量为 0.2)的变换进行拟合。要选择适当的 λ 值,将为这些变换中的每一个变换计算似然函数。计算的假设前提是:误差是独立的,服从均值为 0 且方差为 σ2 的正态分布。将选择使似然函数最大化的 λ 值。该值还使误差平方和在 λ 值中最小。使用二次插值找到围绕具有最小误差平方和的网格点的两个增量网格点之间使似然值最大化的 λ 值。
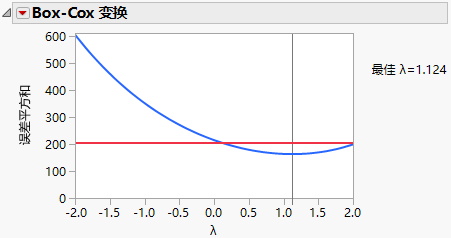
“Box-Cox 变换”报表显示一个图,其中显示 λ 的值与误差平方和 (SSE) 值的对应关系。该图上的水平红线表示 λ 的单侧 95% 置信区间。该置信区间基于 Box and Cox (1964, p. 216) 中定义的置信区域。置信区域用以下不等式定义:
创建一个新的数据表,其中包含从 –2 到 2(以 0.2 为增量)的所有 λ 的参数估计值和误差平方和值。
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
确保次数框的值为 2。
|
|
5.
|
|
6.
|
点击运行。
|
|
7.
|
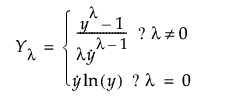
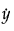 表示几何均值。
表示几何均值。