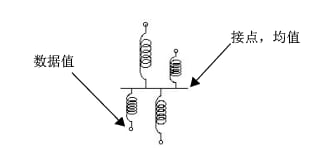
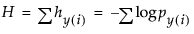首先，弹簧是连续响应模型的拟合装置 (Farebrother 1987)。假定您有 n 个点，想知道这些点的期望值（均值）。设想您将点排列在标尺上并使用弹簧将它们连接到公共接头（请参见图 A.7）。当您放开弹簧时，弹簧上下摆动接点，然后在均值处停下来。根据物理学原理，这是必然发生的事。
图 A.7 将弹簧连接到数据点
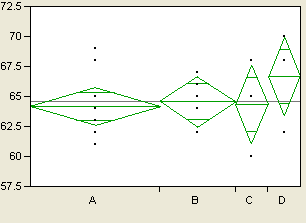
拟合受假设约束时，您通过测量这个相同的弹簧能量来检验假设。假定您在实验中有来自四个不同处理的响应，想检验均值是否有显著差异。首先，假定您的数据已分组标绘（如图 A.8中所示），但是使用弹簧连接每个处理的单独均值。然后施加压力来抗拒弹力，使各个均值向公共均值移动。移好了！限制均值成为相同的能量大小就是所需的检验统计量。该能量是检验均值是否相同的假设的 F 检验的主要组成部分。
图 A.8 连续响应变量的单因子图
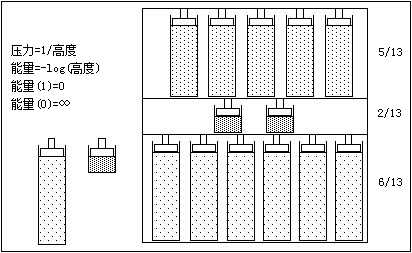
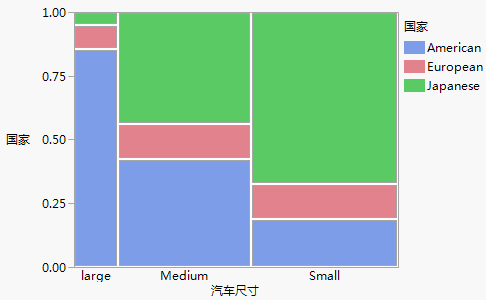
图 A.9显示诸如 medium 类型车的单个类别的情形（请参见图 A.10中Carpoll.jmp 中标记为 medium 的马赛克列）。假定有 13 个响应（小汽车）。第一个水平 (American) 具有 6 个响应，第二个水平具有 2 个响应，最后一个水平具有 5 个响应。响应概率分别变为 6/13、2/13 和 5/13，因为针对响应分割区的压力相抵以使总能量最小。
图 A.9 分割区中的压力缸效应
像弹簧用于连续数据一样，您可以通过一些因子来分割样本并拟合单独的分割集。然后通过测量需要多少额外能量来促使分割区相等，检验响应率在各组上是否相同。设想按车尺寸对车原产国概率分组的压力缸。强制每个组中的分割区水平对齐所需的能量检验这些变量是否有相同的概率。图 A.10显示了这些分割区。
图 A.10 分类数据的马赛克图
