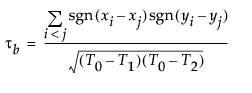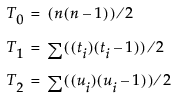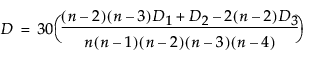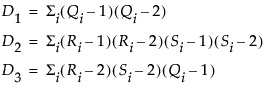该帮助的版本不再更新，请参见https://www.jmp.com/support/help/zh-cn/15.2 获取最新的版本.


多元方法 • 相关性和多元方法 • 计算和统计详细信息 • 关联的非参数测度
上一个
 • 
下一个
关联的非参数测度
对于 Spearman、Kendall 或 Hoeffding 相关性，数据首先要进行秩排序。随后根据数据值的秩执行计算。若存在结值，则使用平均秩。
注意：当指定了“权重”变量时，缺失值和零值权重会从非参数相关性计算中排除。所有其他权重值均视为 1。
Spearman ρ (rho) 系数
使用上述 Pearson 相关性公式基于数据的秩计算 Spearman ρ 相关系数。
Kendall τb 系数
Kendall τb 系数基于一致对和不一致对的数目。若两个变量所对应的一对行对于哪一个变量较大这一点上保持一致，则认为这一对行一致。否则这一对行不一致或为同分对。
公式
计算 Kendall τb，其中：
请注意以下事项：
•
若 z>0，则 sgn(z) 等于 1；若 z=0，则 sgn(z) 等于 0；若 z<0，则 sgn(z) 等于 -1。
•
ti (ui) 是第 i 组 x (y) 结值中的 x (y) 结值的数目。
•
n 是观测数。
•
Kendall τb 的取值范围为 –1 到 1。若指定了权重变量，则它将被忽略。
按照以下方式执行计算：
•
根据第一个变量的值对观测进行秩排序。
•
然后根据第二个变量的值对观测重新进行秩排序。
•
第一个变量的交换次数用于计算 Kendall τb。
Hoeffding D 统计量
Hoeffding D (1948) 的公式如下
其中：
请注意以下事项：
•
Ri 和 Si 分别是 x 值和 y 值的秩。
•
Qi（有时称为二元秩）是 1 加上 x 值和 y 值均小于第 i 个点的点数。
•
在其 x 值或 y 值上有结值的点（而不是这两个值上同时具有结值的点）为 Qi 贡献了 1/2（若其他值小于第 i 个点的相应值）。同时在 x 和 y 上有结值的点为 Qi 贡献了 1/4。
若观测中没有结值，D 统计量的值介于 –0.5 和 1 之间，其中 1 指示完全依赖。若指定了权重变量，则忽略该统计量。