在很多情况下使用 Bagging,其中之一是为了提高预测功效。Bagging 对不稳定的模型特别有用。本例使用 Tiretread.jmp 样本数据表。共有三个因子(硅石、硅烷和硫磺)和四个响应(磨损、弹性系数、伸长和硬度)。首先,您拟合一个神经网络模型来同时预测作为三个因子的函数的四个响应变量。然后,您对神经网络模型执行 Bagging。最后,您比较预测结果,查看通过 Bagging 获得的改进。
|
1.
|
|
2.
|
选择分析 > 预测建模 > 神经。
|
|
3.
|
|
4.
|
|
5.
|
点击确定。
|
|
7.
|
点击执行。
|
|
8.
|
|
1.
|
|
2.
|
从“预测刻画器”旁边的红色小三角菜单,选择保存 Bagged 预测。
|
|
5.
|
点击确定。
|
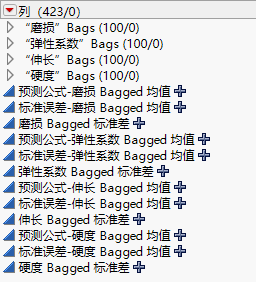
返回数据表。对于每个响应变量,有三个分别表示为预测公式-<列名> Bagged 均值、标准误差-<列名> Bagged 均值、<列名> Bagged 标准差的新列。预测公式-<列名> Bagged 均值列是最终预测。
图 3.31 Bagging 后添加到数据表的列
|
1.
|
选择分析 > 预测建模 > 模型比较。
|
|
2.
|
|
3.
|
|
4.
|
点击确定。
|
|
5.
|
|
6.
|
从“模型比较”旁边的红色小三角菜单,选择标绘“预测值-实际值”图。
|
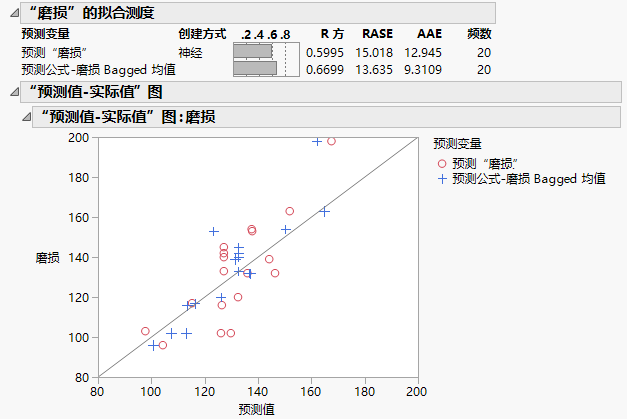
图 3.32 磨损预测的比较
“拟合测度”报表和“预测值-实际值”图显示在图 3.32中。从 Bagging 得到的预测用蓝色显示。从原始神经网络模型得到的预测用红色显示。通常,Bagging 预测比原始模型预测更接近实际线。因为 Bagging 预测更接近实际线,因此 Bagged 预测的 R 方值 0.6699 高于原始模型预测的 R 方值。您得出结论:Bagging 改进了磨损的预测。
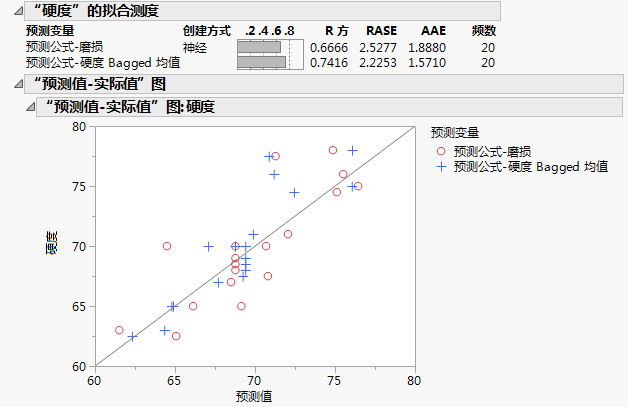
该示例比较了磨损的预测。要比较其他响应变量的预测,请按照第 2 步到第 6 步执行,将磨损替换为所需的响应变量。作为另一示例,图 3.33显示硬度的“拟合测度”报表。该报表显示的结果与磨损的“拟合测度”报表结果相似。Bagged 预测的 R 方值略高于原始模型预测的 R 方值,这说明拟合效果更好,预测得到改进。
图 3.33 硬度预测的比较