本例改编自 Box and Draper (2007),并使用 Stochastic Optimization.jmp。一个化学反应将化学物质 A 转换为化学物质 B,再从 B 转换为 C。化学物质“B”的生成量为反应时间和反应温度的函数。使用刻画器和模拟器探索因子设置以优化 B 的产量。
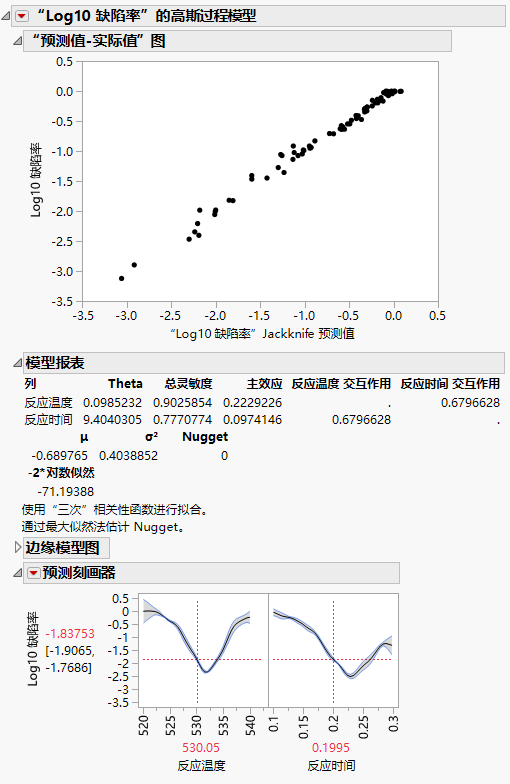
对于该反应,可以使用阿伦尼乌斯定律计算 B 的产量。产量列包含产量的公式。该公式是反应时间(小时)和反应速度 k1 和 k2 的函数。反应速度是反应温度(开氏度)和已知的物理常数 θ1、θ2、θ3、θ4 的函数。因此,产量是反应时间和反应温度的函数。
|
1.
|
|
2.
|
选择图形 > 刻画器。
|
|
3.
|
|
4.
|
|
5.
|
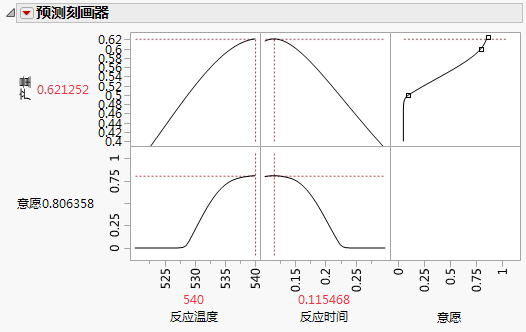
点击“预测刻画器”红色小三角,然后选择最优化和意愿 > 最大化意愿。
|
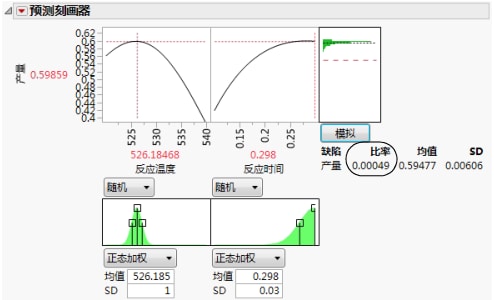
在生产环境中,有时无法精确控制过程输入。若输入(反应时间和反应温度)具有随机变异,产量会有什么变化呢?此外,若产量有规格限,规格外的批次所占百分比是多少?“模拟器”还可以帮助您调查在指定反应时间和反应温度变异的条件下产量的变异和缺陷率情况。
|
1.
|
点击“预测刻画器”红色小三角,然后取消选择最优化和意愿 > 意愿函数。
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
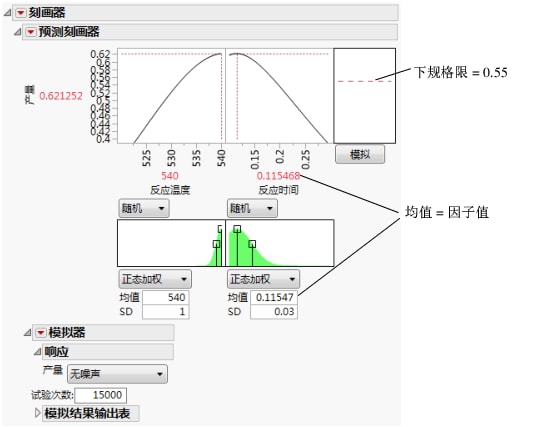
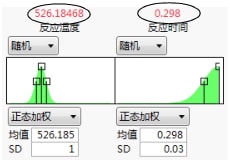
将试验次数值设置为 15,000。
|
|
6.
|
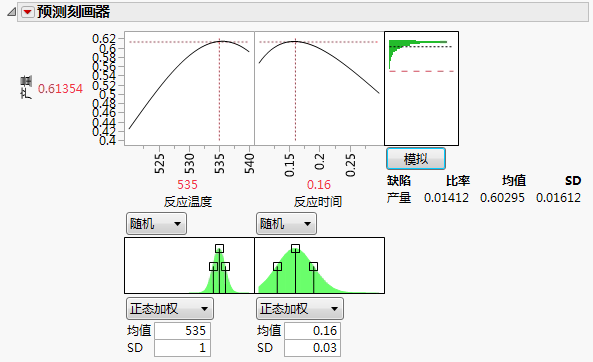
点击模拟按钮。
|
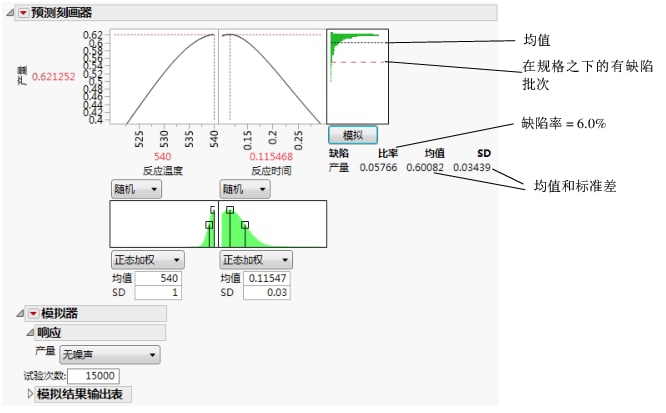
对于“反应温度”540 和“反应时间”0.115,预测的产量为 0.62。在假定温度和时间存在变异的条件下,模拟估计的平均缺陷率约为 6%,标准差为 0.03。缺陷率 6.0% 指示约有 6.0% 的批次将超出规格。
|
7.
|
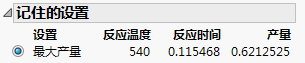
点击“预测刻画器”红色小三角并选择因子设置 > 记住设置。
|
|
8.
|
键入“最大产量”并点击确定。
|
|
9.
|
将反应温度的均值设置为 535。
|
|
10.
|
将反应时间的均值设置为 0.16。
|
|
11.
|
点击模拟。
|
通过对输入因子设置稍作更改,缺陷率降至大约 1.8%,预测产量降低不足 0.01。使产量最大化的固定(无变异性)设置与存在因子变异时缺陷率最小化的设置不同。
|
1.
|
点击“模拟器”红色小三角并选择模拟实验。
|
|
3.
|
点击确定。
|
|
5.
|
|
6.
|
点击传输回因子设置按钮。
|
|
8.
|
点击“预测刻画器”红色小三角并选择因子设置 > 记住设置。
|
|
9.
|
键入“最小缺陷”并点击确定。
|
|
10.
|
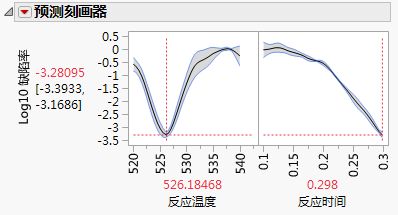
指定新设置后,点击模拟按钮以估计新设置下的缺陷率。
|
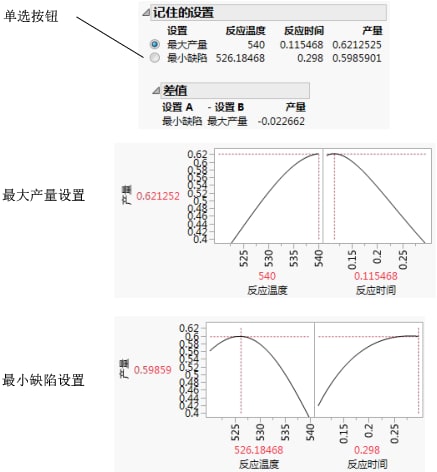
在新设置下,缺陷率为 0.05%,比使产量最大化的设置下的 6.0% 低很多。这几乎降低了大约 120 倍。我们回想一下,第一种设置下的平均产量为 0.62,而新平均产量为 0.59。缺陷率降低 120 倍的代价是平均产量减少了 0.03。
|
11.
|
点击记住的设置单选按钮可以查看每种设置的刻画器。
|
化学家现在知道了将哪个设置用于质量过程。若因子没有变异,则使产量最大化的设置为高温下快速反应。但是,若该过程输入有类似于我们模拟的变异,使产量最大化的设置会导致高的缺陷率。因此,要在有因子变异的情况下使缺陷率最小化,设置应为低温下慢速反应。