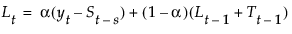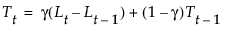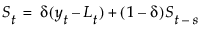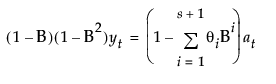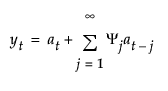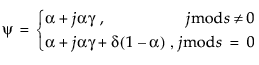μt 是时变均值项
βt 是时变斜率项
s(t) 是 s 时变季节性项中的一项
at 是随机扰动项
每个平滑模型定义一组递归平滑方程,用于描述这些估计量的变化过程。平滑方程是由被称为平滑权重的模型参数定义的:
α 是水平平滑权重
γ 是趋势平滑权重
ϕ 是趋势阻尼权重
δ 是季节性平滑权重
具有单个平滑权重 α 的平滑方程定义如下:
该模型等价于按以下方式定义的一个季节性 ARIMA(0, 1, s+1)(0, 1, 0)s 模型:
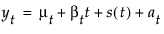
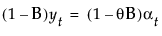 其中,
其中,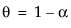
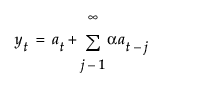
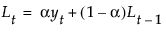
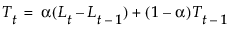
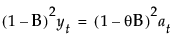 ,其中
,其中 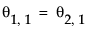 且
且 
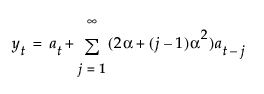
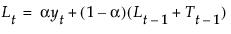
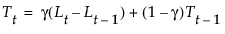
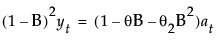 ,其中
,其中 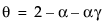 且
且 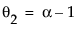
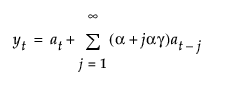
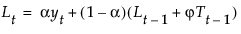
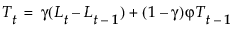
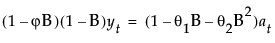
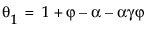
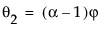
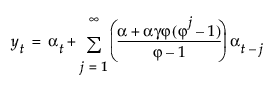
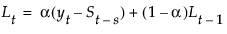
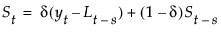
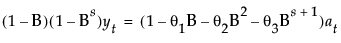
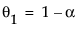
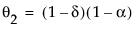
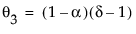
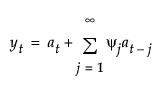 其中,
其中,