|
1.
|
|
2.
|
选择分析 > 质量和过程 > 过程能力。
|
|
3.
|
|
4.
|
|
5.
|
打开分布选项分级显示项。
|
|
6.
|
|
7.
|
点击设置过程分布。
|
后缀 &分布(最佳拟合) 添加至右侧列表中的每个列名。
|
8.
|
点击确定。
|
随即显示一个能力指标图，其中显示 Ppk 值。请注意，只有厚度变量显示在表示 Ppk = 1 的那条线的上方。纯度几乎就位于这条线上。尽管测量值数目 250 看似较大，估计的 Ppk 值仍然变异较大。出于此原因，您需要为真正的纯度 Ppk 值构造置信区间。
|
9.
|
从“过程能力”红色小三角菜单中，选择单项详细报表。
|
|
‒
|
重量：对数正态
|
|
‒
|
厚度：Johnson Sb（请参见“厚度(Johnson) 能力”报表标题正下方的注释）
|
|
‒
|
纯度：Weibull
|
要使用“模拟”实用程序估计 Ppk 置信限，您需要构造反映拟合 Weibull 分布的模拟公式。若不想遵循以下步骤，您可以通过运行添加模拟列表脚本来获取这一部分中的结果。
图 11.27 纯度的 Weibull 参数估计值
|
2.
|
|
3.
|
|
4.
|
|
5.
|
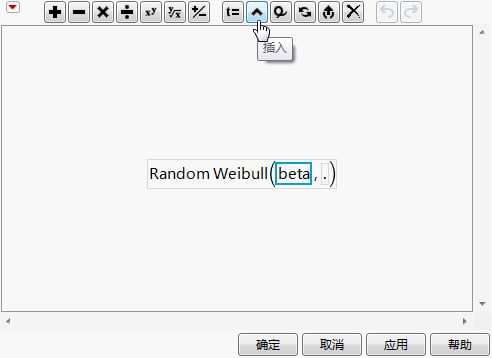
在公式编辑器中，选择随机 > 随机 Weibull。
|
|
6.
|
这将会添加参数 alpha 的占位框。
|
7.
|
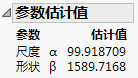
在“参数估计值”报表中右击并选择制成数据表。
|
|
8.
|
复制估计值列第 2 行中的条目 (1589.7167836)。
|
|
9.
|
|
10.
|
在您从“参数估计值”报表创建的数据表中，复制估计值列的第一行中的条目 (99.918708989)。
|
|
11.
|
图 11.29 完成的公式窗口
|
12.
|
在公式编辑器窗口中点击确定。
|
|
13.
|
在“新建列”窗口中点击确定。
|
模拟纯度列包含模拟来自最佳拟合分布的值的公式。
使用“模拟”时，将按照您指定的次数运行整个分析。为缩短计算时间，您可以通过仅运行所需的分析尽量减少计算负担。在本例中，由于您只对具有拟合的 Weibull 分布的纯度感兴趣，所以运行“模拟”之前，您只执行该分析。
|
1.
|
在“过程能力”报表中，从“过程能力”红色小三角菜单中选择重新启动对话框。
|
|
3.
|
|
4.
|
点击删除。
|
|
5.
|
点击确定。
|
|
6.
|
从“过程能力”红色小三角菜单中，选择单项详细报表。
|
同时提供了 Ppk 值和 Ppl 值，但是这些值相同，因为纯度仅有下规格限。
|
7.
|
|
8.
|
|
9.
|
|
10.
|
点击确定。
|
计算过程需要几秒钟的时间。随即显示名为“过程能力模拟结果（估计值）”的数据表。该表中的 Ppk 和 Ppl 列各自包含基于模拟纯度公式计算的 500 个值。第一行（已排除）包含最初分析中得到的纯度的值。由于纯度仅有下规格限，所以 Ppk 值与 Ppl 值相同。
|
11.
|
在“过程能力模拟结果（估计值）”数据表中，点击分布脚本旁边的绿色小三角。
|
图 11.30 纯度的模拟 Ppk 值的分布
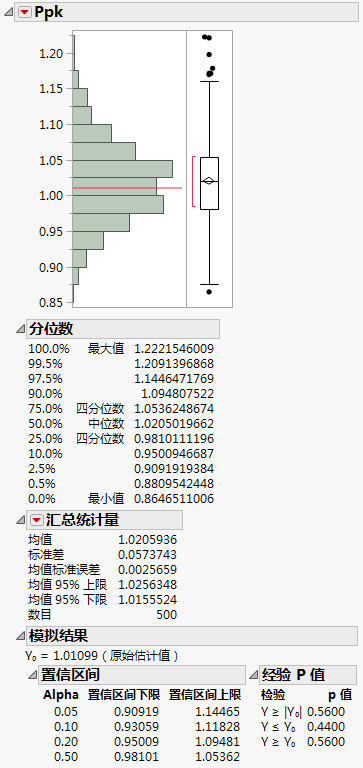
显示了两个分布报表，一个针对 Ppk，另一个针对 Ppl。但是纯度仅有下规格限，所以 Ppk 与 Ppl 的值相同。出于此原因，两个分布报表完全相同。
“模拟结果”报表显示 Ppk 的 95% 置信区间介于 0.909 到 1.145 之间。真正的 Ppk 值可能高于 1.0，那么纯度就会位于您在非正态能力分析中构造的“能力指标图”的 Ppk = 1 线条上方。
|
12.
|
|
13.
|
|
14.
|
|
15.
|
点击确定。
|
|
16.
|
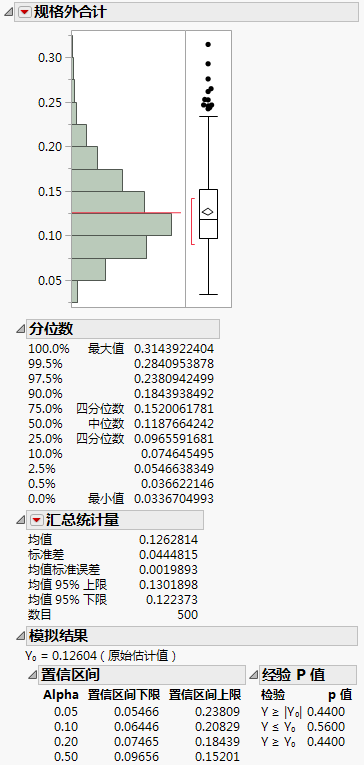
在“过程能力模拟结果（期望总体百分比）”数据表中，点击分布脚本旁边的绿色小三角。
|
图 11.31 纯度的模拟规格外合计值的分布
