LSL = 下规格限
USL = 上规格限
T = 目标值
注意:使用默认的 AIAG (Ppk) 标签时,基于“总 Sigma”的指标表示为 Pp、Ppl、Ppu 和 Ppk。若使用“总 Sigma”,指标 Cpm 的标签不变。本节中的公式使用 Cp 标签定义。
Cp 的 100(1 - α)% 置信区间计算如下:
df 是自由度
N 是观测数
对于“总 sigma”能力,自由度等于 N - 1。
对于具有平衡子组的组内 Sigma 能力,自由度的计算取决于组内 sigma 估计方法。通过无偏标准差的平均值估计的组内 sigma 时,N - m 需要乘以 0.875 和 1 之间的比例因子。请参见 Bissell (1990)。通过极差平均值估计组内 sigma 时,使用基于子组样本大小的公式计算自由度。请参见 David (1951)。
Cpk 的 100(1 - α)% 置信区间计算如下:
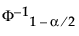 是标准正态分布的第 (1 - α/2) 个分位数
是标准正态分布的第 (1 - α/2) 个分位数N 是观测数
df 是自由度
对于“总 sigma”能力,自由度等于 N - 1。
对于具有平衡子组的组内 Sigma 能力,自由度的计算取决于组内 sigma 估计方法。通过无偏标准差的平均值估计的组内 sigma 时,N - m 需要乘以 0.875 和 1 之间的比例因子。请参见 Bissell (1990)。通过极差平均值估计组内 sigma 时,使用基于子组样本大小的公式计算自由度。请参见 David (1951)。
Cpm 的 100(1 - α)% 置信区间计算如下:
N 是观测数
T 是目标值
s 是 sigma 估计值
Cpl 和 Cpu 的上下置信限使用 Chou et al. (1990) 中的方法计算。
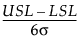
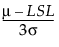
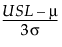
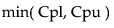
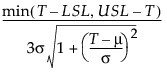
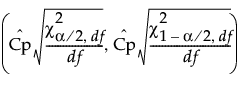
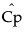 是 Cp 的估计值
是 Cp 的估计值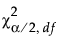 是具有
是具有 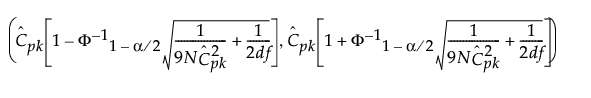
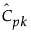 是 Cpk 的估计值
是 Cpk 的估计值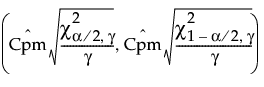
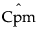 是 Cpm 的估计值
是 Cpm 的估计值 是具有
是具有 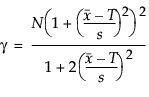
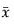 是观测的均值
是观测的均值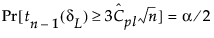 其中
其中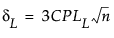
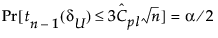 其中
其中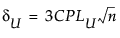
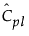 是 Cpl 的估计值
是 Cpl 的估计值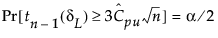 其中
其中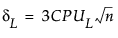
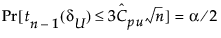 其中
其中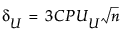
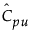 是 Cpu 的估计值
是 Cpu 的估计值